Eigenschaften eines Graphen
Mit dieser allgemeinen Beschreibung ist ein Graph sehr offen definiert. Je nach Anwendung müssen Graphen spezielle Eigenschaften haben. Davon gibt es eine Vielzahl. Im Bildungsplan wird die Einführung der Begriffe "gerichtet/ungerichtet", "gewichtet/ungewichtet" und "zyklenfrei" gefordert. Hier werden weitere Begriffe erläutert, um die Vielfalt der Anwendungen abzudecken und geeignet beschreiben zu können. Sie müssen im Unterricht aber nicht eingeführt werden.
Eine ausführlichere Übersicht hat Manfred Nitzsche in seinem empfehlenswerten Buch „Graphen für Einsteiger“ in Form eines „Kleinen Wörterbuches der Graphentheorie“ zusammengestellt.7
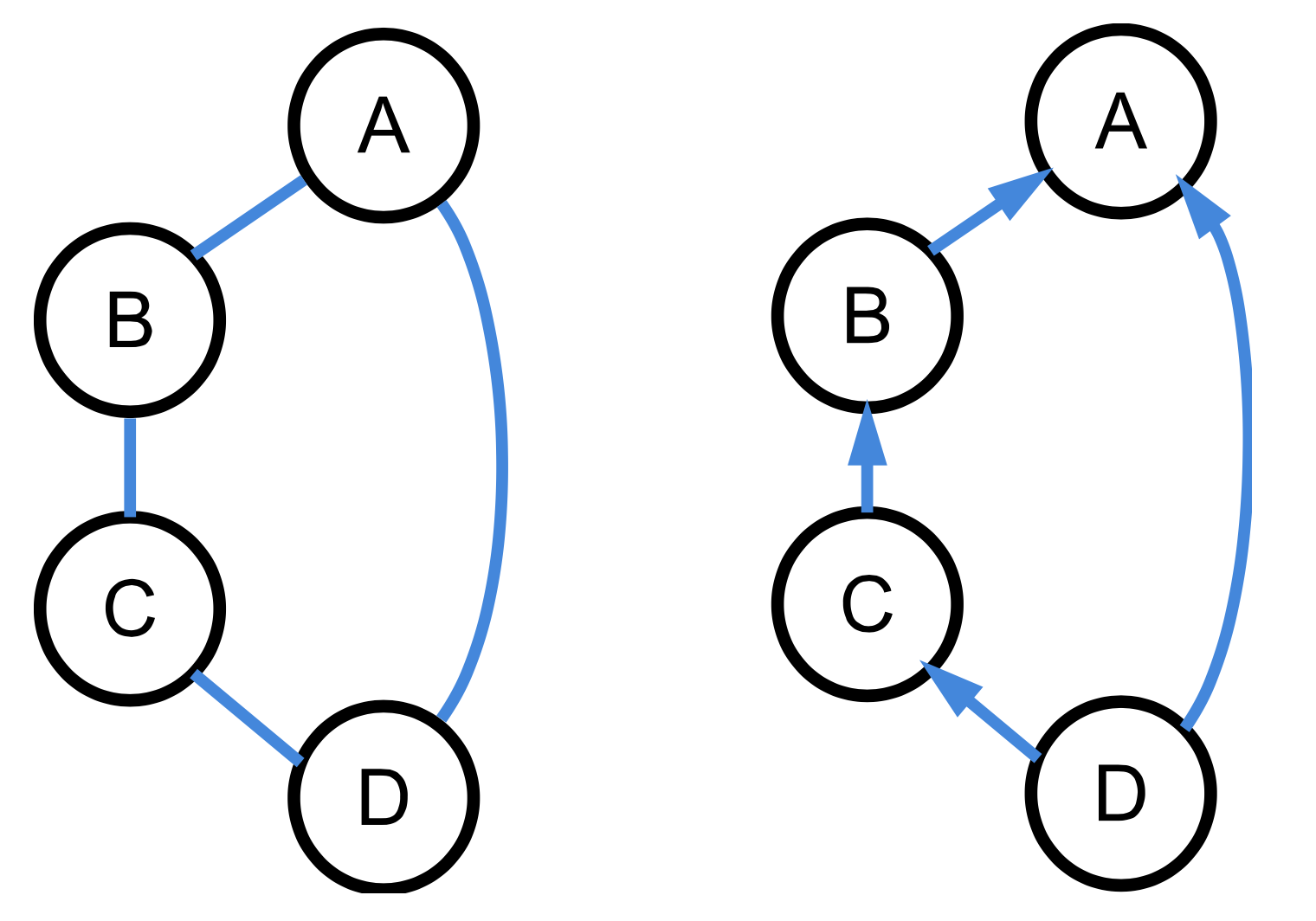
Abbildung 2: ungerichteter Graph / gerichteter GraphZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt
Digraphen
Man unterscheidet ungerichtete von gerichteten Graphen, bei denen Kanten nur in ausgewiesenen Richtungen durchlaufen werden dürfen. Diese Graphen werden auch als Digraph (Directed Graph) bezeichnet.
Mathematisch betrachtet ist eine gerichtete Kante ein (geordnetes) Tupel zweier Knoten, eine ungerichtete Kante eine (ungeordnete) Menge zweier Knoten.
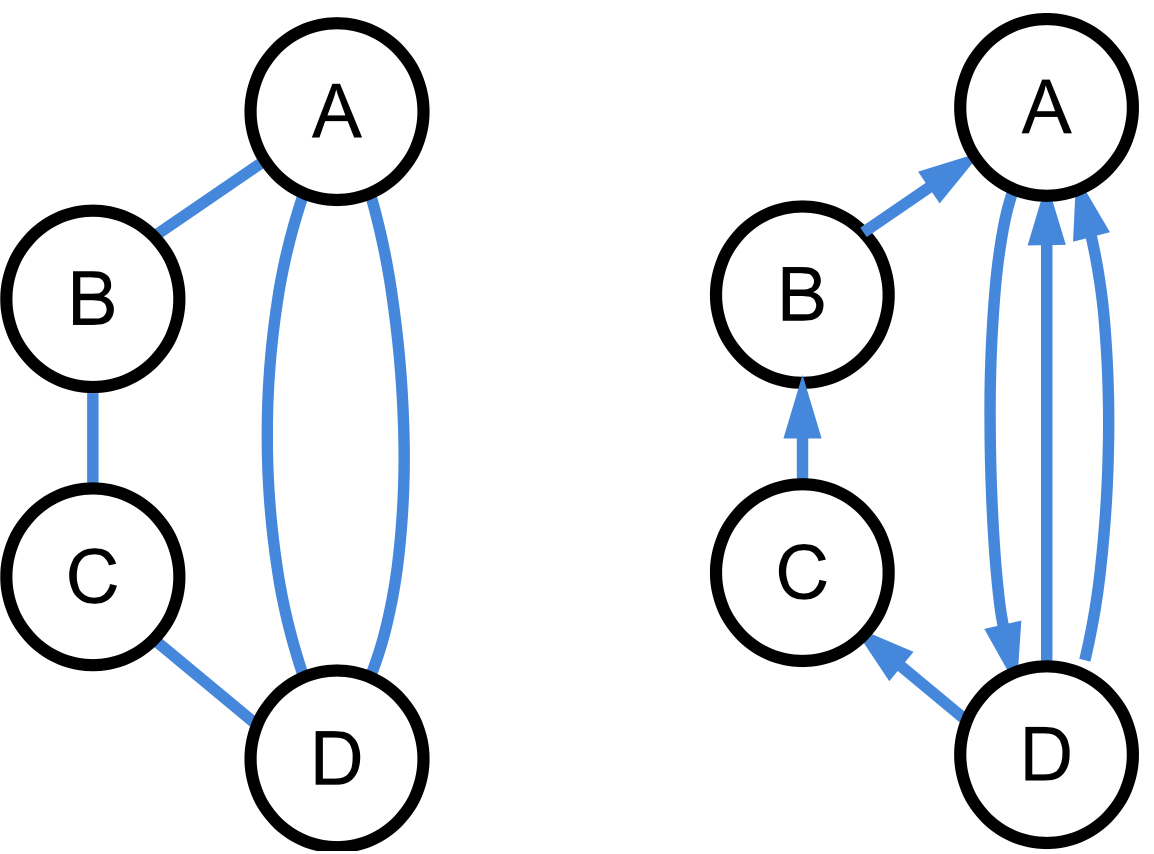
Abbildung 3: ungerichteter Multigraph / gerichteter Multigraph ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt
Multigraphen
Normalerweise gibt es zwischen zwei Knoten maximal eine Kante. Bei Multigraphen ist auch mehr als eine Kante zugelassen.
Ungerichtete Graphen ohne Mehrfachkanten nennt man auch häufig schlicht oder einfach. Meist lässt man aber die Bezeichnungen "ungerichtet" und "ohne Mehrfachkanten" einfach weg.
Grad eines Knoten
Der Grad eines Knotens gibt an, wie viele Kanten ein Knoten hat. In nebenstehendem Beispiel hat der Knoten A beispielsweise den Grad 4 und der Knoten E den Grad 2.
Bei gerichteten Graphen unterscheidet man zwischen Eingangsgrad (auch Innengrad), d.h. der Anzahl der zum Knoten hinführenden Kanten, und Ausgangsgrad (auch Außengrad), d.h. der Anzahl der vom Knoten wegführenden Kanten.
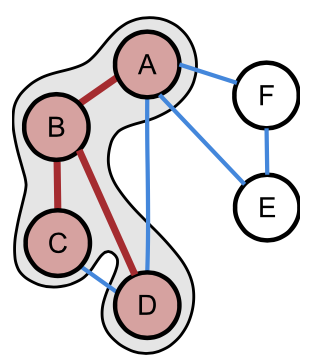
Abbildung 4: Teilgraph ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt
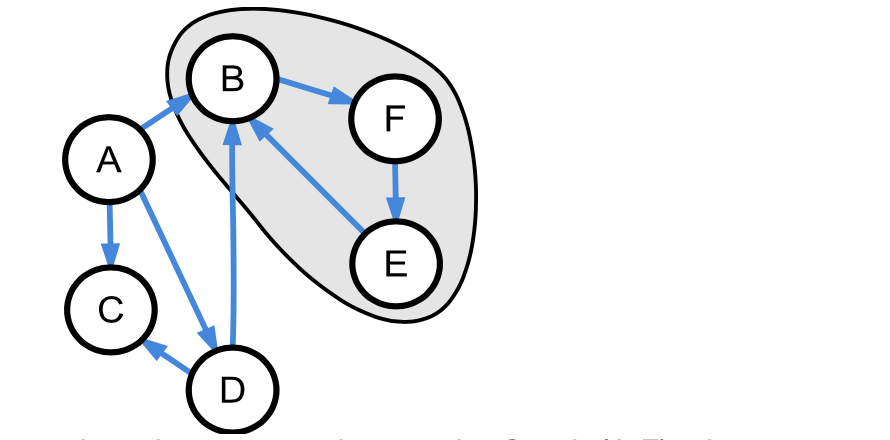
Teilgraph
Ein Teilgraph ist eine Teilmenge der Knotenmenge und der Kantenmenge des Graphen. Dabei dürfen natürlich keine Kanten vorhanden sein, die zu Knoten gehören, die nicht in der Knotenteilmenge enthalten sind.
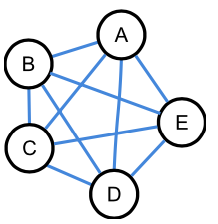
Abbildung 5: vollständiger Graph mit 5 Knoten ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt
Vollständiger Graph
In einem vollständigen Graph ist jeder Knoten mit jedem anderen Knoten durch genau eine Kante verbunden. Der Grad jedes Knoten ist damit bei n Knoten genau n-1.
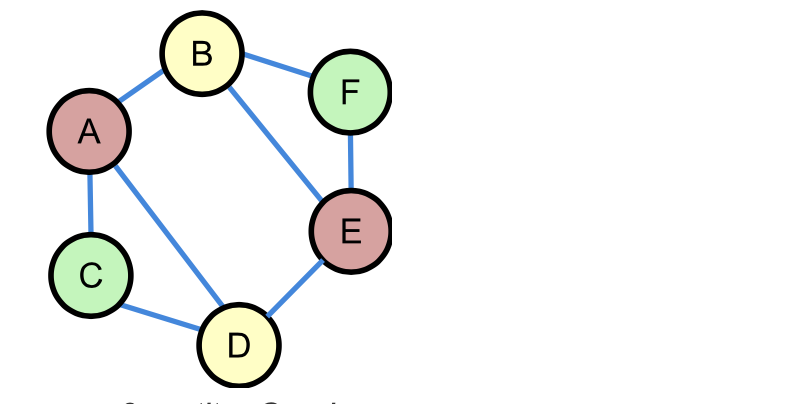
Einen vollständigen Teilgraphen nennt man eine Clique. Diese Benennung ist gut nachvollziehbar, wenn man mit dem Graphen soziale Beziehungen darstellt. In Abbildung 4 würden A, E und F eine Clique bilden.
Wege in Graphen
In der Graphentheorie bezeichnen die Begriffe Weg, Pfad, Kantenzug oder Kantenfolge eine Folge von Knoten, in welcher jeweils zwei aufeinander folgende Knoten durch eine Kante verbunden sind. Leider sind diese Begriffe nicht synonym und werden in der Literatur teilweise nicht einheitlich verwendet. Wir verwenden sie folgendermaßen: Bei einem Kantenzug dürfen Knoten und Kanten mehrmals durchlaufen werden, bei einem Weg oder Pfad darf dagegen jeder Knoten nur einmal enthalten sein. Diese Bedeutungsunterschiede müssen im Unterricht vom Lehrer berücksichtigt werden.
Ein kritischer Pfad ist ein Weg maximaler Länge in einem zyklenfreien, gerichteten Graphen. Kritische Pfade sind entscheidend, wenn es darum geht, zu beurteilen wie lange eine Abfolge von Aktionen maximal dauern kann.
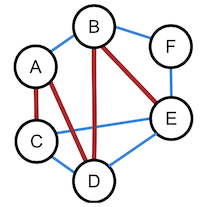
Abbildung 6:
Pfad / Kantenzug
kritischer Pfad der Länge 4
ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt
Zusammenhängender Graph
Ein Graph heißt zusammenhängend, wenn es von jedem Knoten einen Weg zu jedem anderen Knoten gibt.
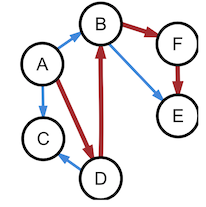
Bei gerichteten Graphen muss man dabei unterscheiden, ob die Richtung der Kanten berücksichtigt werden soll: Bei stark zusammenhängenden Graphen muss es einen Weg unter Berücksichtigung der Kantenrichtung geben. Bei schwach zusammenhängenden Graphen reicht es, wenn es einen Weg im zugehörigen ungerichteten Graphen gäbe.
Ein zusammenhängender Teilgraph wird als Zusammenhangskomponente bezeichnet.
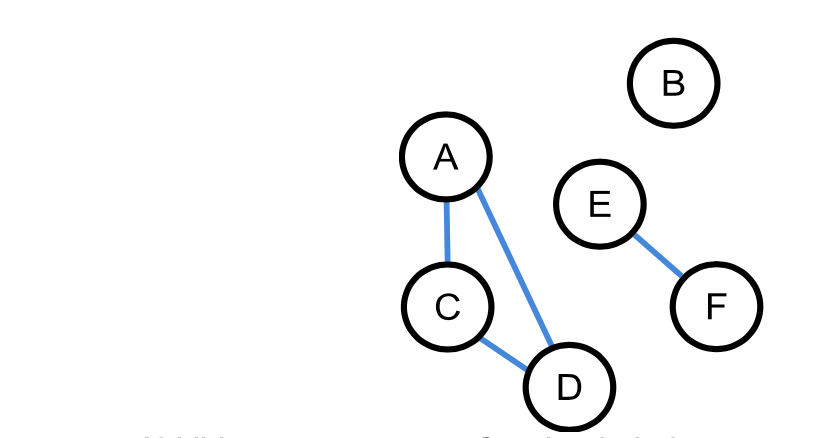
Abbildung 7:
Graph mit drei Zusammenhangskomponenten
schwach zusammenhängender Graph (A-F) mit
starker Zusammenhangskomponente (B-F-E)
ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt
Ein 2-zusammenhängender (k-zusammenhängender) Graph hat für jeden Knoten 2 (k) Wege zu jedem anderen Knoten, die über unterschiedliche Knoten verlaufen. Durch Entfernung eines beliebigen Knotens bleibt der Graph dadurch immer noch zusammenhängend. Das ist z.B. für das Internet sehr wichtig, um Ausfallsicherheit zu gewährleisten.
Zyklenfreier Graph
Ein Zyklus ist ein geschlossener Kantenzug in einem Graphen, d.h. Start- und Endknoten sind gleich. Kommt im Zyklus jeder Knoten maximal einmal vor, d.h. der Kantenzug ist ein Weg, dann bezeichnet man den Zyklus als Kreis. Graphen ohne Zyklen heißen zyklenfrei oder azyklisch. Ein zyklenfreier, zusammenhängender Graph ist immer ein Baum. Ein zyklenfreier Graph mit mehreren Zusammenhangskomponenten wird als Wald bezeichnet. Er besteht aus mehreren Bäumen.
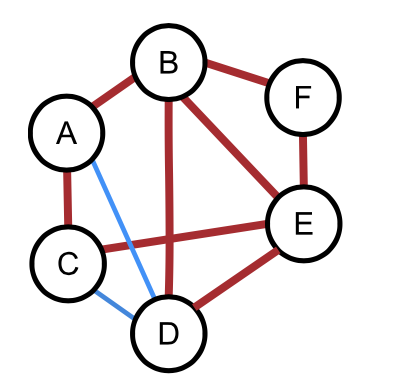
Abbildung 8:
Zyklus in einem Graph
(C-A-B-F-E-D-B-E-C)
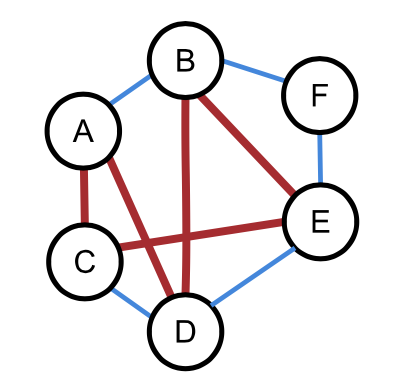
Kreis in einem Graph
(C-A-D-B-E-C)
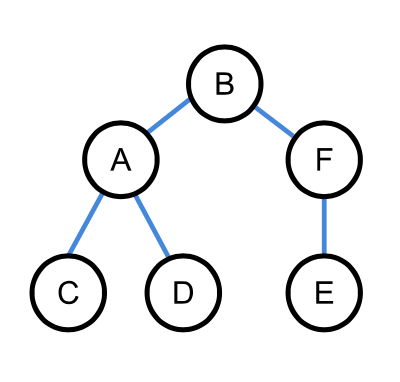
zyklenfreier Graph=Baum
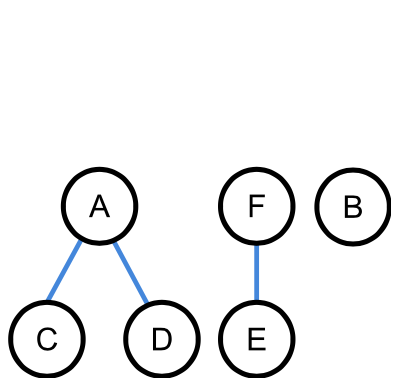
Wald aus 3 Bäumen
ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt
Planare Graphen
Ein planarer Graph lässt sich so darstellen, dass die Kanten sich nicht kreuzen. Die Bezeichnung erklärt sich, wenn man das Färbe-Problem betrachtet.
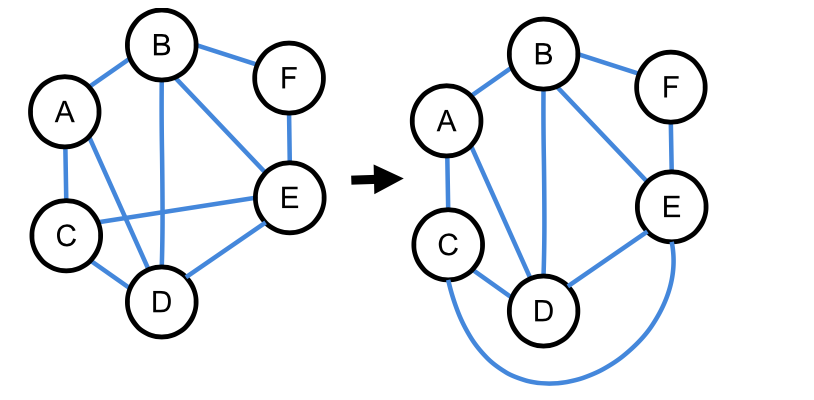
Abbildung 9:
planarer Graph mit isomorpher Umformung
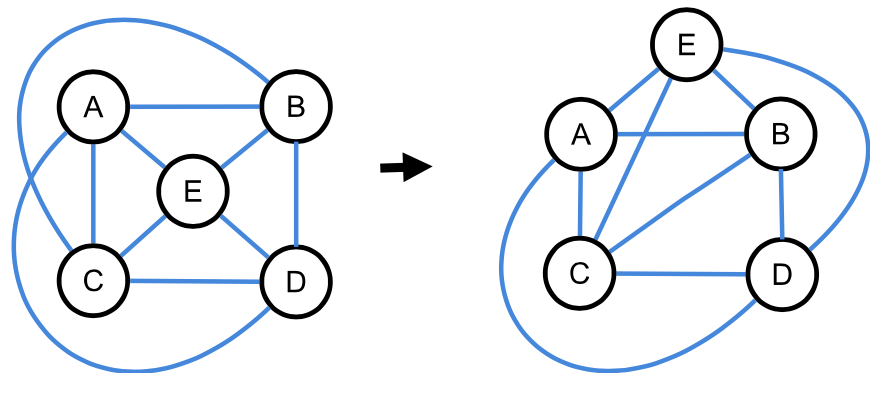
nicht planarer Graph, da es keine kreuzungsfreie isomorphe Umformung gibt
ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt
k-partiter Graph
Ein Graph wird als bipartit bezeichnet, wenn sich die Knoten so in zwei Teilmengen aufteilen lässt, dass innerhalb einer Teilmenge keine zwei Knoten miteinander verbunden sind. Entsprechend sind sie k-partit, wenn die Kontenmenge sich in entsprechend in k Teilmengen aufteilen lässt.
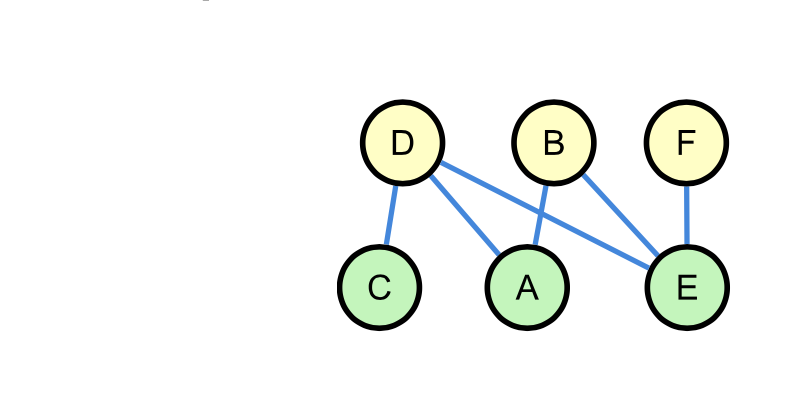
Abbildung 10:
bipartiter Graph
3-partiter Graph
ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt
Gewichtete Graphen
In gewichteten Graphen bekommt jede Kante noch eine Zusatzinformation - ein Gewicht. Dieses Gewicht kann z.B. die Länge der Kante darstellen. Es ist aber auch möglich, über das Gewicht anzugeben, wie viele Kanten zwischen zwei Knoten existieren.
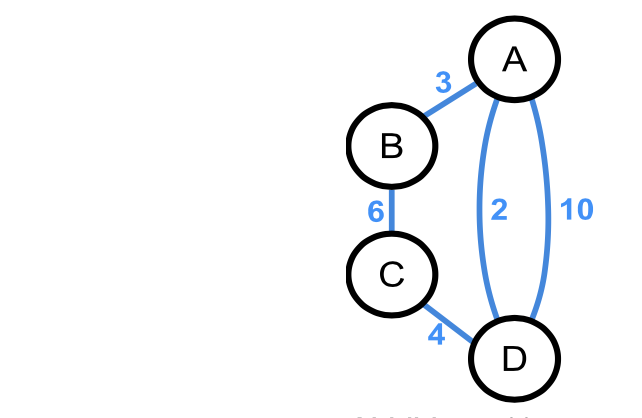
Abbildung 11:
gewichteter Graph
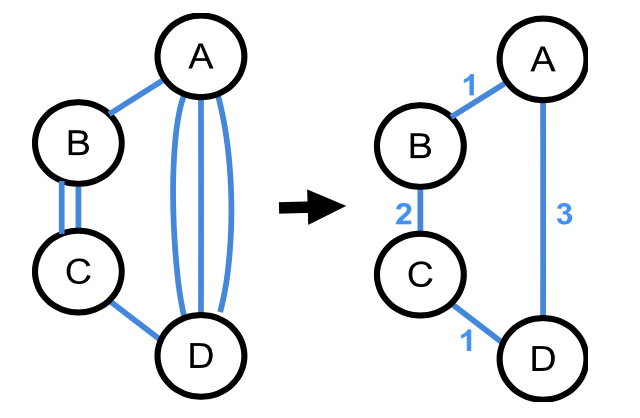
Multigraph: Darstellung durch Gewichte
ZPG Informatik [CC BY-SA 4.0 DE], aus 1_graphen_hintergrund.odt
7 Vgl. „Kleines Wörterbuch der Graphentheorie“, in Nitzsche: „Graphen für Einsteiger“, Vieweg+Teubner, Wiesbaden, 2009, 3. Auflage
Hintergrundinformationen: Herunterladen [odt][990 KB]
Weiter zu Repräsentation eines Graphen
