Problem des kürzesten Pfades in gewichteten Graphen
Begriffe: gewichtete Kanten, Dijkstra-Algorithmus oder Bellman-Ford-Algorithmus
Wenn es bei der Bestimmung des kürzesten Pfades nicht nur um die Anzahl der benutzten Kanten, sondern auch um deren Gewicht geht, muss der Algorithmus verändert werden. Das Gewicht kann dabei die Länge der Strecke zwischen zwei Punkten sein (kürzeste Strecke) oder auch der Zeitbedarf (schnellste Strecke).
Dies leisten der Dijkstra-Algorithmus, der den IMP-Schülern schon bekannt sein müsste, und der Bellman-Ford-Algorithmus.
Dijkstra-Algorithmus: In IMP wurde der Algorithmus anhand der Ameisen-Analogie (gemäß "Abenteuer Informatik" von Jens Gallenbacher) eingeführt. Um auch den IMP-Schülern einen anderen Zugang zu bieten, kann jetzt der Algorithmus als Erweiterung des Algorithmus von Moore angesehen werden: Man behält die Idee bei, dass beim nächsten Knoten die aktuelle Entfernung plus die Länge des Weges dorthin eingetragen werden muss. Allerdings kann es nun sein, dass eine bereits eingetragene Entfernung angepasst werden muss, da man einen kürzeren Weg gefunden hat. Auch die Abarbeitung der ToDo-Liste muss man modifizieren. Um sicherzustellen, dass man nie einen Knoten bearbeitet, dessen Entfernung zum Startknoten nachträglich nochmals angepasst wird, muss man immer denjenigen Knoten aus der ToDo-Liste auswählen, der die kürzeste Entfernung zum Startknoten hat. Bei der Implementation kann man das erreichen, indem man die ToDo-Liste immer nach aufsteigenden Entfernungen sortiert und dann den ersten Knoten nimmt. Das ist keine effiziente Implementierung, aber hier am leichtesten zu bewerkstelligen.
Da die Erweiterung von Moore zu Dijkstra nicht so schwierig ist, wäre es an dieser Stelle möglich, die Schülerinnen und Schüler mit dem Quelltext von Moore starten und die Erweiterung des Dijkstra selbst implementieren zu lassen. Alternativ kann auch der Moore-Algorithmus selbst ausgehend von textueller Beschreibung oder Pseudocode implementiert werden.
Bellman-Ford-Algorithmus:
Der Bellman-Ford-Algorithmus geht ähnlich vor. Wenn vom Startknoten zu einem Knoten ein Pfad gefunden wurde, wird bei den Nachbarknoten kontrolliert, ob der Weg über diesen Knoten dorthin kürzer ist, als der bisher kürzeste Weg. Man versucht dabei aber nicht, die Bearbeitungs- reihenfolge der Knoten so zu wählen, dass ein schon bearbeiteter Knoten nicht erneut bearbeitet werden muss. Stattdessen werden so viele Durchgänge durchgeführt, dass nachträgliche Änderungen an einem Knoten erneut an alle Folgeknoten weitergegeben werden können. In einem Durchgang wird dabei jede Kante einmal betrachtet. Daher kann man eine Schleife über alle Kanten statt einer Schleife über alle Knoten verwenden.
Wählt man als Anzahl der Durchgänge die Knotenzahl des Graphen, stellt man sicher, dass die kürzesten Wege zu allen Knoten gefunden wurden. Im ungünstigsten Fall verläuft der längste kürzeste Weg zu einem Knoten über alle anderen Knoten. Mehr Zwischenschritte sind nicht möglich, da es im Normalfall nicht sinnvoll ist, einen Zyklus (mehrfach) zu durchlaufen. Nur bei Zyklen, die ein negatives Kantengewicht haben, würde sich die Gesamtstrecke durch den Zyklus verkürzen. Es würde sich lohnen den Zyklus immer wieder zu durchlaufen. Daher erkennt man diese (verbotenen) Zyklen daran, dass ein weiterer Durchgang nach Beendigung des Algorithmus eine weitere Verbesserung der Wege bringen würde. Einzelne Kanten mit negativen Kantengewichten sind aber erlaubt.
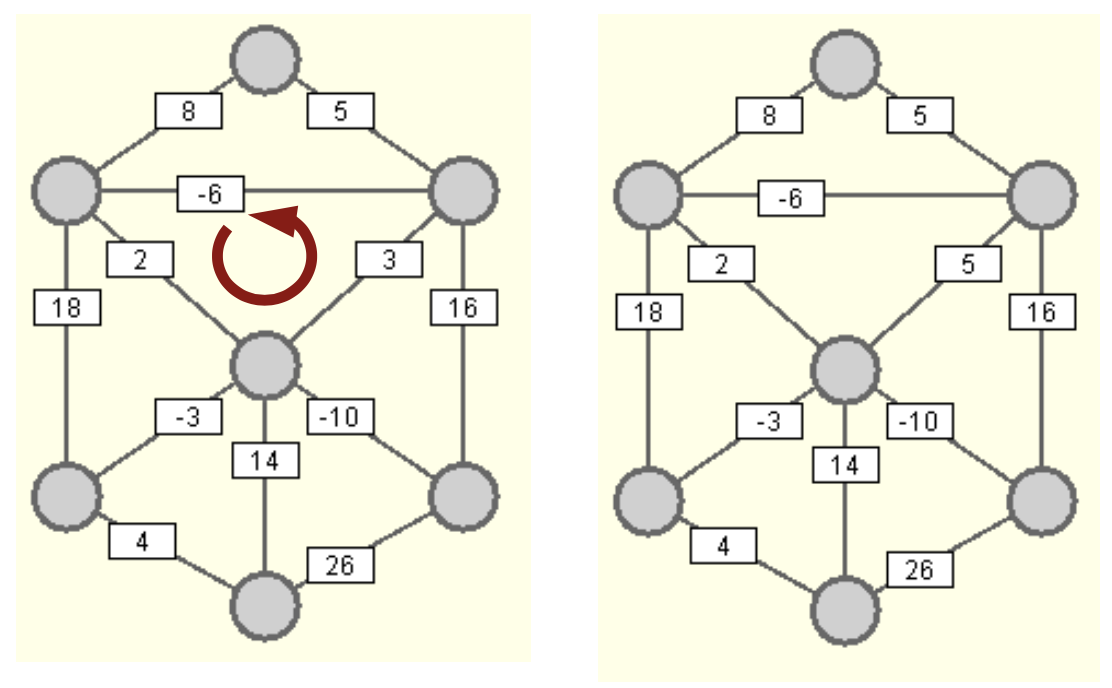
Bildquelle: Graphen mit negativen Kantengewichten: Der erste Graph ist nicht zulässig, da der rot markierte Zyklus das Gewicht -1 hat. (eigenes Werk) ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 2_unterrichtsverlauf.odt
Am Ende sollte auf jeden Fall das Schulwegbeispiel mit dem Algorithmus ausgewertet und mit dem ersten Entwurf verglichen werden. Man könnte die Schüler auch noch weitere Wege im Modell einfügen (z.B. den Friedhof) oder die Gewichtung von Bundesstraßen oder Fußgängerzonen im Modell verändern lassen und der Auswirkung bei der Bestimmung der Wege untersuchen lassen. Beispiele mit gerichteten Kanten oder negativen Gewichten befinden sich im Ordner 04_routenplanung.
Ergänzung: Dynamisches Routing (Distanz-Vektor-Verfahren)
Die Laufzeit des Bellman-Ford-Algorithmus ist schlechter als die des Dijkstra-Algorithmus. Seine große Stärke liegt aber darin, dass er auch funktioniert, wenn man jeden Knoten als eigenständigen Akteur betrachtet, der mit seinen Nachbarknoten kommunizieren kann. Er fragt seine Nachbarn immer wieder nach deren Entfernung zum Startknoten und passt seine eigene Entfernung gegebenenfalls an. Machen das alle Knoten, stellt sich nach einer gewissen Zeit ein stabiler Zustand ein, in dem die kürzesten Entfernungen vom bzw. zum Startknoten bekannt sind. Die Gesamtstruktur des Graphen muss dazu nicht bekannt sein. Jeder Knoten muss nur seine Nachbarknoten kennen.
Tauscht man nicht nur Information über die Entfernung zu einem Knoten aus, sondern zu allen Knoten (man übergibt dann einen Distanz-Vektor), kennt man am Ende die kürzesten Entfernungen zu allen Knoten und weiß, über welchen nächsten Knoten der Weg verläuft. Diese Information ist für das Routing im Internet notwendig.
Dieses Distanz-Vektor-Verfahren kann man gut mit Schülern durchspielen, indem jeder Schüler einen Knoten "spielt" und eine Karte mit seinen Nachbarknoten und den Gewichten der Kanten dorthin bekommt. Der komplette Graph wird noch nicht benötigt/gezeigt. Die Schüler teilen ihren Nachbarn ihren Distanz-Vektor immer wieder mit, bis sich keine Änderungen mehr ergeben. Dann müssten die kürzesten Entfernungen von allen Knoten zu jedem anderen Knoten gefunden sein. Dies überprüft man durch Einblenden des gesamten Graphen.
Mit Hilfe des Tools "DistanzVektorAlgorithmusGenerator.exe" (Ordner 06_software) von Rainer Helfrich (RP Tübingen) kann man für bis zu 14 Schüler einen Graphen zufällig generieren und für jeden Schüler Excel-Vorlagen für die Routing-Tabellen und Distanzvektoren erzeugen lassen. Zunächst gibt man die Namen der Schüler (einen pro Zeile) ein und generiert einen Graphen. Diesen kann man abspeichern und später wieder laden. Dann lässt man mit "Blätter erzeugen" die Excel-Tabellen erstellen und druckt sie aus. Für die Durchführung des Rollenspiels empfiehlt es sich zur besseren Übersicht, wenn jeder Schüler zwei Ablagen für „eingehende“ und „ausgehende“ Distanzvektor-Blätter auf dem Tisch hat.
Nachdem die Schüler das Rollenspiel beendet haben, kann man das Ergebnis kontrollieren, indem man den Graph anzeigt. Ein Doppelklick auf einen Knoten des Graphen zeigt die kürzesten Entfernungen zu den anderen Knoten an. Wählt man einen Zielknoten rechts unten, wird der Pfad in der Graphenansicht gezeigt.
Ergänzung: Vergleich mit anderen Verfahren
Die Schülerinnen und Schüler haben in Computerspielen oft Kontakt mit Gegnern, die sich ihre Wege zu einem selbst suchen. Dabei können die Spielfiguren meist nicht nur entlang von Straßen mit Kreuzungen laufen, sondern kreuz und quer über eine Karte bewegen. Je nach Untergrund manchmal schneller oder langsamer. Die folgenden beiden Webseiten zeigen, dass auch in diesem Fall die besprochenen Algorithmen verwendet werden können. Dabei wird ein quadratisches Raster über die Karte gelegt. Jedes Quadrat ist ein Knoten. Je nach Einstellung sind nur die direkt daneben liegenden Quadrate oder auch die diagonal angrenzenden Quadrate mit Kanten verbunden.
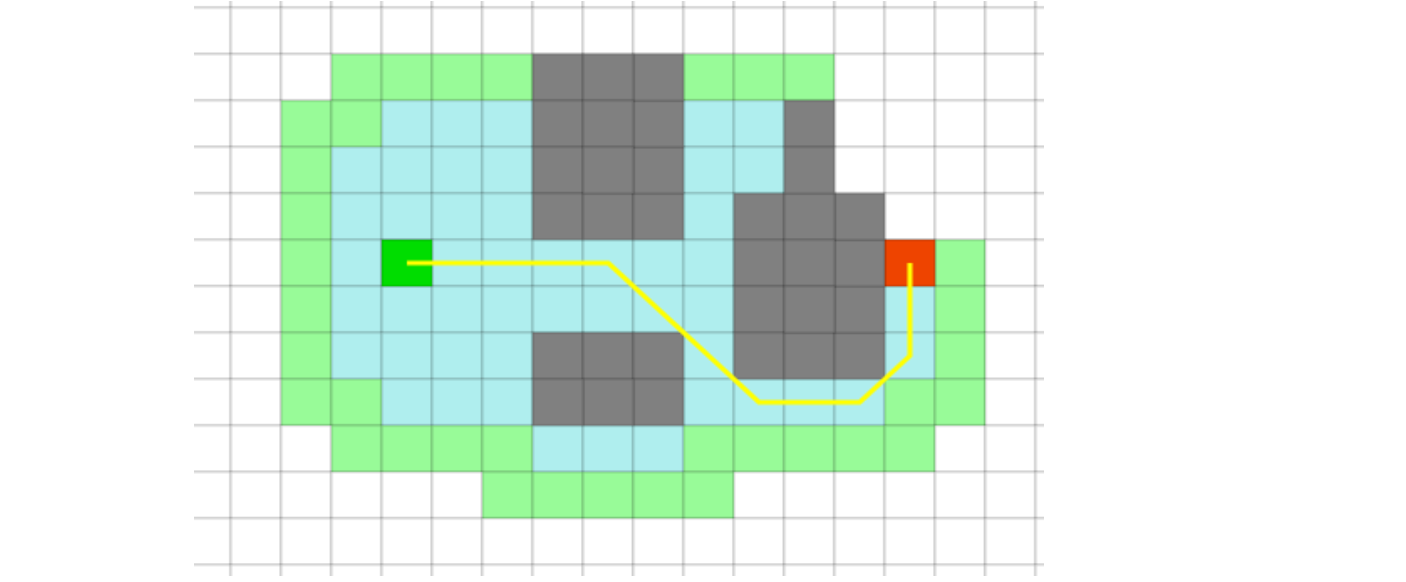
Bildquelle: Wegbestimmung mit PathFinding.js, Xueqiao Xu (MIT Licence), URL: https://qiao.github.io/PathFinding.js/visual/ (abgerufen 04.11.2020) ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 2_unterrichtsverlauf.odt
Die Applets zeigen dabei schön, wie viele Knoten zur Bestimmung des Weges ausgewertet wurden. Außerdem können weitere Algorithmen ausprobiert werden (z.B. Best-First-Search: ein Greedy-Algorithmus, der in jedem Schritt versucht, die Entfernung zum Ziel zu minimieren).
PathFinding.js: https://qiao.github.io/PathFinding.js/visual/
Introduction to the A* Algorithm: https://www.redblobgames.com/pathfinding/a-star/introduction.html
Unterrichtsverlauf: Herunterladen [odt][298 KB]
Weiter zu Dominierende Mengen
