Abstrakte Datentypen

Ein Abstrakter Datentyp (ADT) ist zunächst einmal ein Verbund von Objekten. Er verrät nichts über seinen inneren Aufbau, sondern erlaubt den Zugriff auf die enthaltenen Objekte ausschließlich mittels seiner Methoden. Diese Methoden sind über ihre Signatur definiert, also z.B. die Methode enthaelt(val: T): boolean. Hier ist festgelegt, dass die Methode mit dem Namen enthaelt einen Parameter des Typs T hat und einen Wert des Typs boolean zurückgibt. Eine Klasse, die einen ADT darstellen soll, muss alle definierten Methoden⁶enthalten. Dies entspricht zunächst einmal dem Konzept der abstrakten Klassen bzw. Interfaces.

Ein ADT definiert zusätzlich noch eine bestimmte Semantik, d.h. man erwartet, dass der Aufruf einer Methode einen bestimmten Effekt hat, der unabhängig von der darunterliegenden Implementation ist. Ein Programmierer, der bei einer Liste die Methode anhaengen aufruft, erwartet, dass der neu angehängte Wert sich unmittelbar danach an der letzten Stelle der Liste befindet.

Es ist möglich, das Verhalten von ADTs über Axiome zu definieren, z.B. für den ADT Stack:

x sei ein beliebiges Element, s sei ein Stack, die Funktion emptyStack() erzeuge einen leeren Stack. Dann gelten die folgenden Gleichungen⁷ , die das Verhalten von pop(), push() und top() beschreiben:

```
isEmpty(emptyStack()) = true
```
Ein neu erzeugter Stack ist leer.
```
isEmpty(push(x,s)) = false
```
Ein Stack, auf den etwas gepusht wurde, ist nicht leer
```
pop(emptyStack()) 
```
→ Fehler

Eine Pop-Operation auf leeren Stacks ist nicht erlaubt
```
pop(push(x,s)) = x
```
Das Ergebnis einer Pop-Operation ist das zuletzt gepushte Element
```
top(emptyStack())
```
→ Fehler

Eine Top-Operation auf leeren Stacks ist nicht erlaubt
```
top(push(x,s)) = x
```
Das oberste Element ist das zuletzt gepushte Element

Diese Definition ist zwar mathematisch korrekt, bildet aber nicht unbedingt die Realität im Unterricht ab. Dies liegt hauptsächlich daran, dass hier ein funktionaler Stil verwendet wird, bei dem z.B. das Ergebnis der Methode push(x: T, s: Stack) ein neuer Stack ist. Jede Datenstruktur, die dieses Verhalten aufweist, kann als Stack bezeichnet werden. Für andere ADTs wie z.B. Liste, Queue und Set gibt es entsprechende Definitionen, die aus einer Sammlung von Methoden und deren erwartetem Verhalten besteht. Es gibt jeweils verschiedene Ansätze, wie man das gewünschte Verhalten erreichen kann. Jeder dieser Ansätze hat Vor- und Nachteile, welchen man verwenden sollte, hängt vom konkreten Anwendungsfall ab. Die Definition der Schnittstellen der ADTs mit ihrem erwarteten Verhalten ist im Dokument 03_definition_adts.odt beschrieben.

Der ADT Liste

Der ADT Liste kann zunächst einmal als verkettete Liste implementiert werden, wie er im Abschnitt „Implementation in Java“ ab Seite 5 beschrieben wurde. Das Listen-Objekt hält dabei nur eine Referenz auf den Anfang der Liste.

Dadurch kann durch Verfolgen der Nachfolger-Verweise jedes Element der Liste erreicht werden. Die Methoden können dabei sowohl iterativ als auch rekursiv implementiert werden.

Vorteile:

Der Speicherbedarf ist direkt proportional zur Anzahl der Elemente der Liste.
Das Einfügen und Entfernen am Anfang geht schnell (unabhängig von der Listenlänge)

Nachteile:

Für jedes Element muss der Nachfolgerverweis gespeichert werden.
Der wahlfreie Zugriff auf Elemente (Einfügen, Auslesen und Entfernen) ist umso aufwendiger, je weiter hinten sie in der Liste stehen.
Das Bestimmen der Länge ist aufwendig.

Als Variante der obigen Herangehensweise könnte die Liste zudem einen Verweis auf das letzte Element speichern. Dies erhöht in manchen Fällen die nötigen Schritte beim Einfügen und Entfernen von Werten, allerdings stets nur um einen konstanten Zusatzaufwand. Dafür ist das Einfügen am Ende in konstanter Zeit möglich, da der Verweis auf das letzte Element bereits bekannt ist.

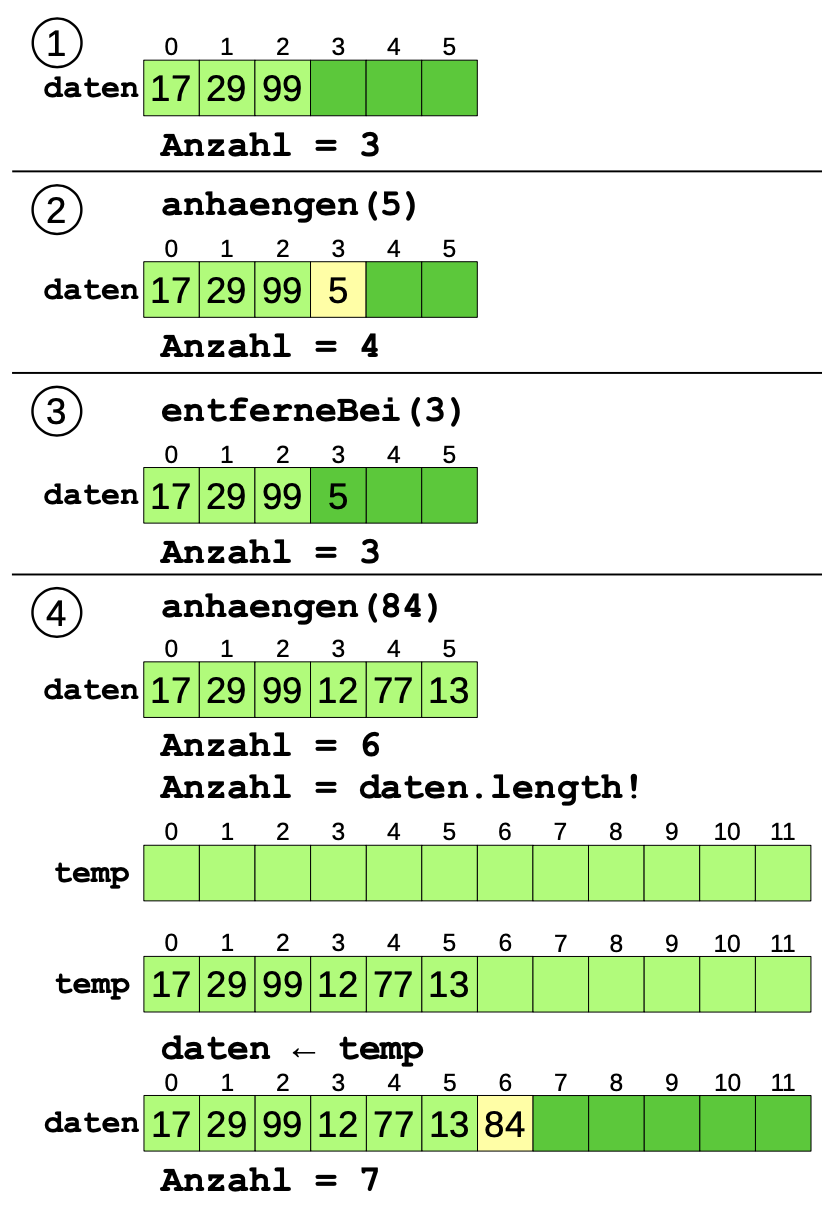
Bildquelle: Hashtabelle ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 02_hintergrund_adts.odt

Ein anderer Implementierungsansatz basiert auf einem Array⁸ . Die Liste enthält ein Array von Werten, das z.B. beim Erzeugen des Objekts mit 6 Plätzen initialisiert wird. Zudem verwendet man eine Variable (im Beispiel rechts „Anzahl“), die speichert, wie viele der Plätze des Arrays mit gültigen Werten belegt sind.

Beim Anhängen eines Wertes wird dieser einfach an die Stelle geschrieben, die durch „Anzahl“ benannt wird; dann wird diese um 1 erhöht. Entfernt man das letzte Element, reicht es, die Anzahl um 1 zu verringern. Dass weiterhin ein alter Wert im Array steht, stört nicht, da die Methoden des ADTs keine Möglichkeit bieten, auf diesen zuzugreifen.

Aufwendiger ist es dann allerdings, Werte weiter vorne in die Liste einzufügen. Dabei müssen alle dahinter stehenden Werte um eine Stelle nach rechts gerückt werden, damit ein Platz frei wird. Umgekehrt rücken die Elemente eine Stelle nach links, wenn dort ein Wert entfernt werden soll.

Wenn irgendwann das Array „voll belegt“ ist und weitere Werte eingefügt werden sollen, muss man ein neues Array anlegen, das z.B. doppelt so groß ist. Die alten Werte werden in das neue Array kopiert und die Liste verwendet fortan das neue Array als Daten-Array. Diese Operation ist zwar sehr aufwendig, kommt aber relativ selten vor. Zudem kann man die Größe des Arrays beim Erzeugen bereits auf einen bestimmten Wert setzen, wenn man abschätzen kann, wie viele Elemente die Liste ungefähr maximal enthalten wird.

Vorteile:

Relativ geringer Speicherbedarf
Anhängen, Längenbestimmung und lesender Zugriff auf beliebige Elemente sind schnell möglich

Nachteile:

Unter Umständen wird zu viel Platz verwendet, wenn nur wenige Elemente enthalten sind.
Entfernen und Einfügen vorne sind zeitaufwendig

Der ADT Stack

Ein Stack arbeitet nach dem „last-in-first-out“-Prinzip (LIFO). Das bedeutet, dass Elemente nur aus einer Richtung eingefügt („push“) und entfernt („pop“) werden können und sich die Reihenfolge der Elemente nicht ändert. Das zuletzt in den Stack eingefügte Element muss dadurch als erstes wieder entfernt werden, bevor man auf irgendwelche darunterliegenden Elemente zugreifen kann. Zudem ist es möglich, das oberste Element des Stacks nur zu betrachten („top“).

Stacks werden in der Fachliteratur auch als „Keller“ oder „Stapel“ bezeichnet. Die Vorstellung dahinter ist ein enger Kellerraum, in dem man Kisten nur von einer Seite abstellen kann und auf die dahinterliegenden Kisten keinen Zugriff hat, bis man die vorderen herausgeräumt hat.

Die wichtigste Anwendung von Stacks ist der „call stack“. Details finden sich im Kapitel Rekursion (ab Seite 17 dieses Dokuments).

Stacks lassen sich ebenso wie Listen mit Verkettung implementieren. Dabei entspricht das oberste Element des Stacks dem ersten Element der Liste. Auf diese Weise ist das Ablegen und Entfernen von Elementen schnell möglich und erfordert kein wiederholtes Verfolgen von Nachfolgerbeziehungen.

Bildquelle: ADT Stack ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 02_hintergrund_adts.odt

Auch eine Implementation, die analog zur ArrayList funktioniert, ist möglich. Dabei steht das letzte Element für das oberste Element des Stacks. Eine Push-Operation legt den neuen Wert an die nächste freie Stelle des Arrays und erhöht den Zähler um 1. Ein Pop setzt den Zähler einfach um 1 herunter. Von Zeit zu Zeit kann es auch hier passieren, dass der Stack zu groß wird und ein neues Array angelegt werden muss.

Eine weitere – aber eher theoretische – Implementationsvariante ist die Cantorsche Paarungsfunktion⁹ . Mit Hilfe dieser Funktion und ihrer Umkehrung kann man ebenfalls einen Stack von natürlichen Zahlen simulieren.

Die Paarungsfunktionpackt zwei natürliche Zahlen (x und y) zu einer (z) zusammen. Die Funktion ist umkehrbar: Wenn man zwei Hilfsfunktionen und definiert¹⁰ , kann man x und y wieder „entpacken“:

und

Wenn man nun einen leeren Stack s als die Zahl 2 definiert¹¹ , kann man die Push-Operation push(n) durch die Rechnung s_neu = π(s_alt, n) repräsentieren. Umkehrt entspricht π₂(s) der top()-Operation und s_neu = π₁(s_alt) der pop()-Operation.

In der Praxis ist die Cantorsche Paarungsfunktion nicht brauchbar, da die Zahl, die den Stack-Inhalt repräsentiert, sehr schnell wächst. Wenn man z.B. nur eine 0 pusht, wird .

Wenn größere Zahlen gepusht werden, ist s noch größer. Das bedeutet, die Zahl, die den Stack repräsentiert, wird bei jedem Push etwa quadriert und benötigt damit etwa doppelt so viele Bits, um sie zu speichern. Die Länge des Stacks im Speicher wächst also exponentiell und ist damit nicht mehr in akzeptabler Zeit berechenbar.

Der ADT Queue

Bildquelle: ADT Queue ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 02_hintergrund_adts.odt

Die Queue („Warteschlange“) verfährt nach dem „First-in-first-out“-Prinzip (FIFO): Werte werden „hinten“ eingereiht („enqueue“, „einreihen“) und vorne wird der Wert, der schon am längsten in der Queue enthalten ist, entfernt („dequeue“, „entnehmen“). Zudem kann man sich das vorderste Element ansehen, ohne die Queue zu verändern („front“, „vorderstes“). Auch hier lässt sich die Reihenfolge der Elemente nicht verändern¹² .

Queues sind z.B. für die Durchführung des Breitensuche-Algorithmus auf ungewichteten Graphen notwendig, mit dem man den schnellsten Weg zwischen zwei Knoten finden kann.

Die Implementation der Queue lässt sich – ähnlich wie die Liste – mit Verkettung implementieren. Hier ist es jedoch sehr sinnvoll, einen Verweis sowohl auf den ersten als auch auf den letzten Listenknoten zu halten. Damit ist es möglich, das Einfügen und das Entnehmen mit einer konstanten Anzahl von Schritten durchzuführen. Wenn die Queue sich nur den ersten oder nur den letzten Knoten merkt, muss beim Einfügen oder Entfernen die gesamte Kette durchlaufen werden, um das jeweils andere Ende zu finden.

Auch eine Array-basierte Implementation ist möglich. Um zu vermeiden, dass bei jeder Veränderung alle enthaltenen Elemente verschoben werden müssen, wird eine „Ringpuffer“-Strategie verwendet. Es werden zwei Indizes first und last verwendet, die für die Position des vordersten und des hintersten Elements im Array stehen. Beim Einfügen wird das neue Element an die Position last geschrieben und die Variable wird um 1 erhöht. Zum Entfernen erhöht man first um 1. Sobald first oder last über den letzten gültigen Index wachsen, setzt man sie wieder auf 0 zurück. Sollte nach dem Einfügen first und last gleich sein, bedeutet das, dass das Array tatsächlich voll ist. In diesem Fall kopiert man die Daten in ein neues, größeres Array und passt die Grenzen first und last entsprechend an.

Vergleich von Stack und Queue

Bildquelle: ADTs Stack und Queue ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 02_hintergrund_adts.odt

Wenn man die ADTs Stack und Queue vergleicht, stellt man fest, dass sie eine ähnliche Struktur haben. Jede Operation des Stacks hat eine entsprechende Operation in der Queue und umgekehrt. Abgesehen von der Benennung sind die Methoden sowohl von der Signatur als auch von der Semantik her gleich:

push/enqueue: Fügt einen Wert ein
pop/dequeue: Entfernt einen Wert und gibt ihn zurück
top/front: Gibt den Wert zurück, der als nächstes entfernt werden kann

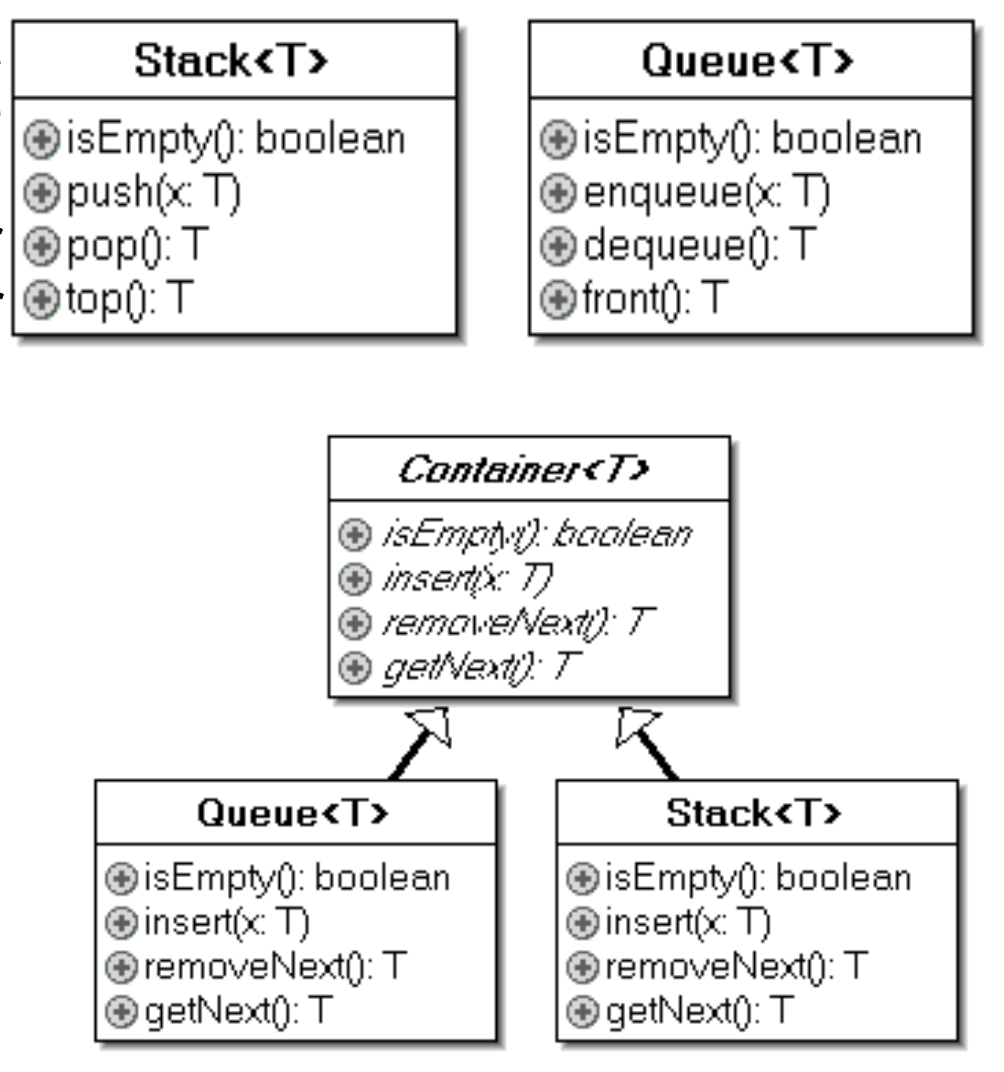
Daher kann man eine gemeinsame Basisklasse „Container“ definieren. Die Methoden von Stack und Queue müssen dabei nur umbenannt werden: push/enqueue → insert, pop/dequeue → removeNext, top/front → getNext

Der ADT Set

Ein Set entspricht einer Menge im mathematischen Sinne. Es kann beliebig viele Werte eines Typs enthalten, wobei es nicht auf die Reihenfolge ankommt und Elemente höchstens einmal vorkommen dürfen. Die Kernfunktionalität eines dynamischen Sets ist im Begleitdokument 03_definition_adts.odt beschrieben. Bei einem dynamischen Set kann man nach dessen Erzeugung noch Elemente hinzufügen oder entfernen. Ein statisches Set hingegen wird bei der Erzeugung einmalig mit Werten gefüllt und ist danach nicht mehr veränderbar.

Die einfachste Implementationsvariante ist, eine ArrayList oder eine der oben beschriebenen Listenvariationen als Container zu verwenden. Diese ist zwar relativ kompakt zu speichern, allerdings ist z.B. die Einfüge-Operation relativ aufwendig, weil zunächst geprüft werden muss, ob der einzufügende Wert bereits enthalten ist. Im ungünstigen Fall muss dazu jedes Element der internen Liste untersucht werden. Auch beim Entfernen muss das Element zunächst einmal gefunden werden.

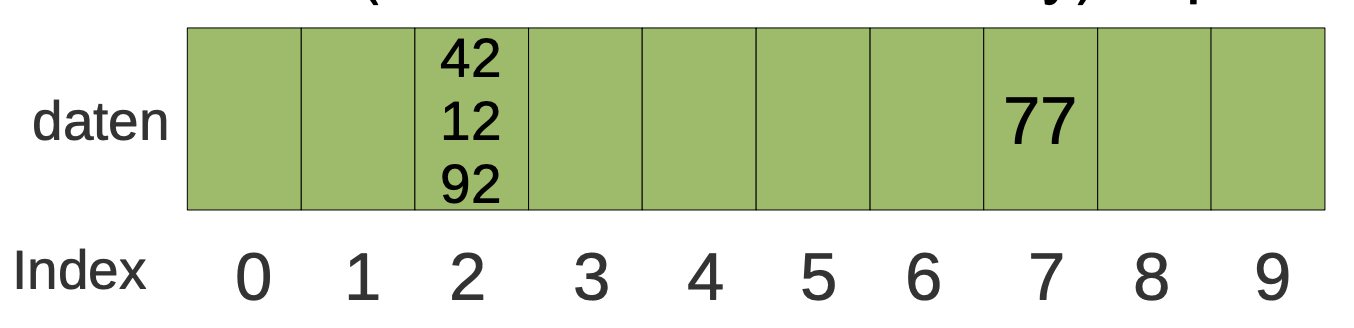
Ein anderer Ansatz ist, eine Hashtabelle zu verwenden. Die Idee dahinter ist, dass man ein Array mit einer festgelegten Länge (z.B. 10) verwendet und einem Wert „ansieht“, wo im Array er liegen müsste. Dazu definiert man eine Hashfunktion h(x) z.B. als h(x) = x mod Arraylänge. Beim Einfügen eines Werts bestimmt man seinen Hashwert und speichert ihn am resultierenden Index:

einfuegen(42): h(42) = 2 einfuegen(77): h(77) = 7

Um zu prüfen, ob ein Wert im Set enthalten ist, bestimmt man dessen Hashwert und vergleicht, ob der dort vorhandene Wert gleich dem gesuchten ist:

enthaelt(42): h(42) = 2, daten[2] == 42 → true

enthaelt(23): h(23) = 3, daten[3] ist leer → false

enthaelt(17): h(17) = 7, daten[7] ist nicht leer, aber daten[7] != 17 → false

Ein Problem ist allerdings, dass die Funktion h nicht injektiv ist: Es gibt eine Vielzahl von Eingabewerten, die zum gleichen Ergebnis führen. Dies folgt aus dem Schubfachprinzip und weil die möglichen Eingaben alle natürlichen Zahlen sind, die Bildmenge aber nur z.B. die Zahlen von 0 bis 9. Ein solcher Fall wird als Kollision bezeichnet.

Um Kollisionen zumindest selten zu machen, kann man die Hashfunktion so gestalten, dass alle Bildwerte im Anwendungsfall etwa gleich häufig auftreten. Dennoch muss der Kollisionsfall durch die Datenstruktur behandelt werden. Eine Möglichkeit dafür ist offenes Hashing mit geschlossener Adressierung¹³. Das Array enthält nicht nur einzelne Werte, sondern kann mehrere Werte enthalten. Man spricht von den Arrayplätzen als „Buckets“ („Behälter“). Diese Behälter müssen beim Suchen eines Werts durchsucht werden. Typischerweise werden diese Behälter als Listen (verkettet oder mit Array) implementiert.

Auf diese Weise muss man zwar weiterhin eine lineare Suche in einem Behälter durchführen, allerdings enthält dieser bei geeigneter Wahl der Hashfunktion nur einen Bruchteil aller Werte im Set. Wenn man zusätzlich noch Rehashing (siehe unten) verwendet, enthält jeder Behälter im Durchschnitt höchstens einen Wert. Es ist zwar theoretisch möglich, dass alle Werte in einem Behälter landen, aber sehr unwahrscheinlich.

Rehashing bedeutet, dass das Set sich den Auslastungsgrad merkt, dies ist die Anzahl der Elemente geteilt durch die Länge des Arrays. Sobald diese Auslastung über z.B. 75% steigt, wird das Array der Behälter vergrößert¹⁴ und die Werte werden neu eingefügt. Diese Operation ist zwar zeitaufwendig, ist aber nur sehr selten nötig.

Da die Hashfunktion in konstanter Zeit berechenbar ist und die Anzahl der Elemente in jedem Behälter im Durchschnitt unter 1 liegt, ist das Einfügen, Suchen und Entfernen sehr schnell möglich. Ein Nachteil ist, dass sehr viel Speicherplatz verschwendet wird.

Das Hashing-Prinzip lässt sich auch auf beliebige Objekttypen erweitern. Dazu muss der Datentyp in Java die Methode hashCode(): int der Klasse Object überschreiben¹⁵ , so dass mit dem Rückgabewert dieser Methode gearbeitet werden kann.

Ein dritter Ansatz wäre, mit Bitmasken zu arbeiten. Dieses Prinzip funktioniert allerdings nur, um Sets von natürlichen Zahlen zu speichern. Die Idee ist, dass eine Menge von natürlichen Zahlen angibt, welche Bits der Zahl auf 1 gesetzt werden.

Bildquelle: Tabelle von ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 02_hintergrund_adts.odt

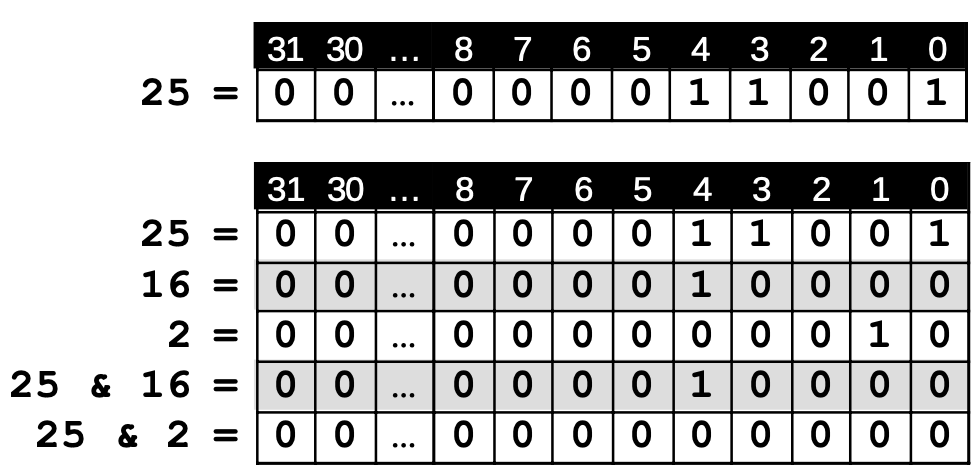
Beispiel: Die Menge { 0, 3, 4 } soll gespeichert werden, indem bei einer Zahl genau die Bits 0, 3 und 4 auf 1 gesetzt werden. Die resultierende Zahl ist 25.

Um zu prüfen, ob eine bestimmte Zahl in der Menge enthalten ist, wendet man die binäre UND-Verknüpfung an:

int vier_gesetzt = 25 & 16; // Ergebnis: 16 != 0

→ 4 ist enthalten

int zwei_gesetzt = 25 & 4; // Ergebnis: 0 == 0

→ 2 ist nicht enthalten

Die benötigte Maske, um zu prüfen, ob die Zahl n enthalten ist, erhält man, indem man die Zahl 1 um n Stellen nach links verschiebt:

int maske = 1 << n;

Bildquelle: Tabelle von ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 02_hintergrund_adts.odt

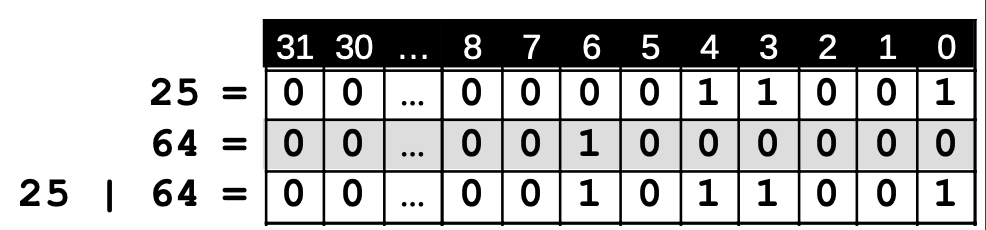
Um weitere Werte zur Menge hinzuzufügen, bildet man die ODER-Verknüpfung der Menge mit einer entsprechenden Maske.

Beispiel: Es soll eine 6 hinzugefügt werden.

int maske = 1 << 6; // 64
menge = menge | maske; // 89

Nach einer Einfüge-Operation darf ein Wert nicht mehrfach vorkommen. Wenn ein Bit bereits gesetzt ist, ändert der ODER-Operator allerdings nichts daran:

menge = menge | 8; // weiterhin 89

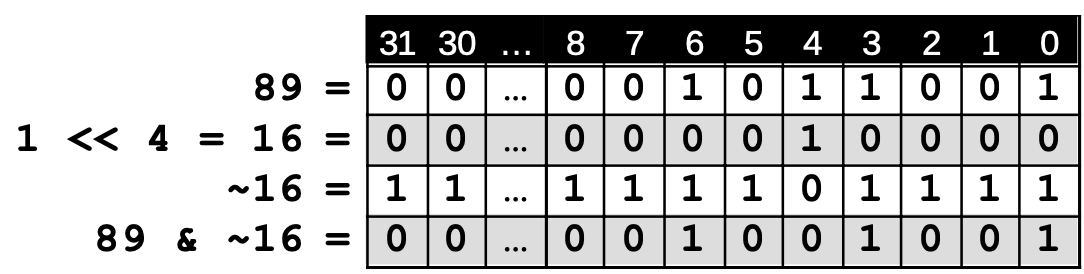
Wenn ein Wert aus der Menge entfernt werden soll, muss man zuerst eine Maske konstruieren, an der das gewünschte Bit auf 0 gesetzt ist und alle anderen auf 1. Dazu verschiebt man zunächst die Zahl 1 um n Stellen nach links und dreht dann alle Bits um (in Java geht das mit dem ~-Operator). Dann wird eine UND-Verknüpfung der Menge mit der Maske durchgeführt.

Bildquelle: Tabelle von ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 02_hintergrund_adts.odt

int maske = 1 << n;
maske = ~maske;
menge = menge & maske;

Beispiel: Die 4 soll aus der Menge { 0, 3, 4, 6 } entfernt werden.

Das Vereinigen und Schneiden von Mengen mit anderen Mengen ist sehr einfach und schnell möglich: Anstelle der durch Bitverschiebung konstruierten Maske nimmt man einfach die andere Menge und führt eine UND- bzw. ODER-Verknüpfung durch.

Bei dieser Technik ist es bisher aber nur möglich, eine Menge von Zahlen zwischen 0 und 31 darzustellen. Um einen größeren Wertebereich zu ermöglichen, verwendet man nicht nur eine Zahl, sondern ein Array oder eine ArrayList von int-Zahlen.

Bildquelle: Tabelle von ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 02_hintergrund_adts.odt

Die Zahl n wird also durch das Bit n mod 32 der Zahl mit dem Index im Array daten repräsentiert.

Wenn daten ein Array ist, muss beim Erstellen eine Größe festgelegt werden. Deshalb muss man festlegen, dass eine Instanz von Set z.B. Zahlen bis zu einer Obergrenze von 100.000 repräsentieren kann. In diesem Fall hat das Array die Länge 100.000/32 = 3125.

Alternativ kann man auch eine ArrayList verwenden, wodurch es keine Obergrenze mehr gibt. Jetzt muss allerdings unter Umständen beim Einfügen die ArrayList mit ausreichend vielen Nullen aufgefüllt werden, damit der neue Wert an die richtige Stelle kommt.

Vorteile der Technik: Bei „dichten“ Mengen (d.h. wenn das Verhältnis zwischen Mächtigkeit der Menge und größtem Wert relativ hoch ist) ist die Speicherung sehr kompakt (theoretisch 1 Bit pro Wert). Der Zugriff beim Lesen und Löschen ist garantiert in konstanter Zeit möglich und sehr schnell.

Nachteile der Technik: Die Technik ist nur auf natürliche Zahlen anwendbar. Beim Einfügen muss unter Umständen die ArrayList mit Werten aufgefüllt werden, was Zeit kostet, wenn ein Wert hinzukommt, der viel größer als das bisherige Maximum ist. Alternativ ist der Wertebereich eingeschränkt. Zudem wird bei dünn besetzten Mengen (wenige Elemente, die ggf. sehr groß sind) viel Platz verschwendet.

⁶ Welche Methoden ein ADT anbietet, kann von den Anforderungen abhängig sein. Für die Set z.B. hängt es davon ab, ob man eine statische oder eine dynamische Set definieren will: https://en.wikipedia.org/wiki/Set_(abstract_data_type)#Operations

⁷ Nach https://de.wikipedia.org/wiki/Abstrakter_Datentyp#Mathematisch-axiomatische_Methode

⁸ Diese Implementationsvariante verwendet z.B. die häufig eingesetzte ArrayList von Java.

⁹ Die Cantorsche Paarungsfunktion kommt z.B. beim Beweis zum Einsatz, dass die Menge der Bruchzahlen gleichmächtig mit der Menge der natürlichen Zahlen ist. In der theoretischen Informatik wird sie auch verwendet, um zu zeigen, dass man einen Stack mit einer Turingmaschine umsetzen kann. Diese Möglichkeit, einen Stack zu konstruieren, ist nicht bildungsplanrelevant.

¹⁰ Die Gaußklammer steht für die Abrundungsfunktion

¹¹ Wenn man den leeren Stack als 0 definieren würde, hätte man das Problem, dass π(0,0) = 0 ist. Ein leerer Stack wäre also nicht von einem Stack unterscheidbar, auf den eine oder mehrere Nullen gepusht wurden. Da π(1,0) = 1 ist, fällt auch der Wert 1 weg.

¹² Eine mögliche Erweiterung ist eine „Priority Queue“, bei der den Elementen ein Zahlwert, die Priorität, zugeordnet ist. Beim Entfernen wird jeweils der Wert mit der höchsten bzw. niedrigsten Priorität entfernt. Die Priority Queue ist z.B. für den Dijkstra-Algorithmus notwendig.

¹³ Das Gegenstück dazu ist „geschlossenes Hashing mit offener Adressierung“. Wenn der eigentliche Ablageort bereits belegt ist, wird hier ein anderer Ablageort gesucht. Bei linearem Sondieren bedeutet das z.B. dass die Felder direkt dahinter abgesucht werden, bis ein freier Platz gefunden ist. Eine spezifische Schwierigkeit hier ist, dass man beim Löschen ehemalig belegte Felder markieren muss.

¹⁴ Man vergrößert z.B. die Arraylänge von n auf 2n+1. Weil n und 2n+1 teilerfremd sind, ist es relativ unwahrscheinlich, dass sich gehäufte Kollisionen nach dem Rehashing wieder häufen.

¹⁵ https://www.codeflow.site/de/article/java-hashcode

Hintergrundinformationen: Herunterladen [odt][305 KB]

Weiter zu Bäume