Bäume
Ein Baum ist – wie die verkettete Liste – eine Datenstruktur, die aus einzelnen Elementen aufgebaut sind, die auf ihre Nachbarn verweisen. Genau wie Listenknoten hat jeder Baumknoten ein Datenelement, das beliebige Werte umfassen kann. Allerdings haben Baumknoten im Unterschied zur Liste mehrere Nachfolgeknoten. Diese werden als Kinder des Knotens bezeichnet. Umgekehrt hat jeder Knoten genau einen Elternknoten, der auf ihn verweist. Die einzige Ausnahme ist der Wurzelknoten, der keine Eltern hat. Auf diese Weise ist vom Elternknoten aus jeder Knoten des Baums durch einen eindeutigen Pfad erreichbar, wenn man wiederholt die Nachfolgerverweise verfolgt. In manchen Implementationen ist es sinnvoll, wenn ein Kindknoten zusätzlich einen Verweis auf seinen Elternknoten besitzt16. Dies macht allerdings die Veränderung des Baumes komplizierter.
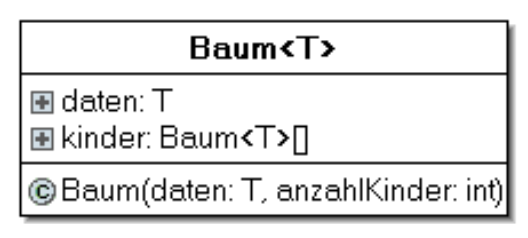
Bildquelle: Baum von ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 02_hintergrund_adts.odt
Bäume sind Spezialfälle von gerichteten Graphen mit der Zusatzeigenschaft, dass jeder Knoten mit Ausnahme der Wurzel den Eingangsgrad 1 hat. Das bedeutet, dass alle Algorithmen, die auf gerichteten Graphen ausgeführt werden können, auch für Bäume anwendbar sind. In diesem Dokument und dieser Unterrichtseinheit wird die Datenstruktur Baum behandelt, nicht der ADT Baum17.
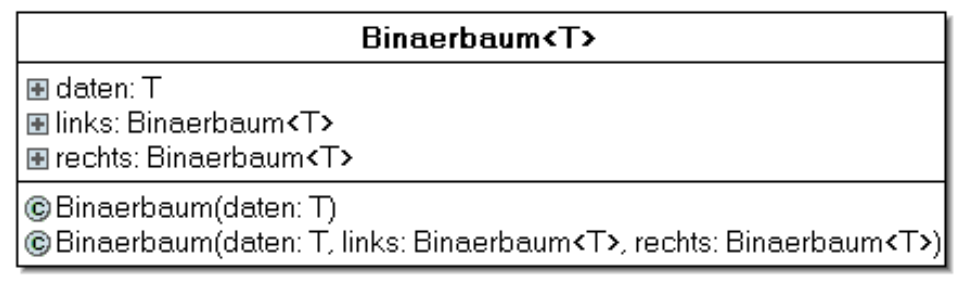
Bildquelle: Binärbäume von ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 02_hintergrund_adts.odt
Ein Spezialfall von Bäumen stellen Binärbäume dar. Hier hat jeder Knoten maximal zwei Kindknoten. Man spricht dann vom „linken“ und „rechten“ Kind(-knoten).
Es gibt in der Informatik eine Vielzahl von Anwendungen von Bäumen. Bäume werden zur Darstellung von Verzeichnishierarchien, Vererbungsbeziehungen, Entscheidungsregeln, Rechentermen, der Struktur von HTML- oder XML-Dateien und vielem mehr verwendet. Mitunter werden die Baumstrukturen nicht explizit aufgebaut, sondern ergeben sich durch rekursive Algorithmen, wie z.B. bei der rekursiven Berechnung der Fibonacci-Funktion oder Spielbäumen.
Traversierungen
Viele Baumalgorithmen erfordern eine vollständige Traversierung des Baumes. Das bedeutet, dass jeder Knoten des Baums nacheinander durchlaufen wird. Es bietet sich an, eine rekursive Implementation zu verwenden.
Beispiel: Ein Binärbaum enthält Zahlen als Datenwerte. Es soll die Summe aller Werte des Baums berechnet werden. summe(b: Binärbaum):
sum = b.daten
falls b.links != null:
sum += summe(b.links)
falls b.rechts != null:
sum += summe(b.rechts)
return sum
Der erste Aufruf der Funktion wird mit der Wurzel des Baumes ausgeführt. Wir gehen davon aus, dass dieser nicht bereits null ist. Bei der Ausführung werden alle Knoten des Baums rekursiv durchlaufen.
Beim Durchlaufen eines Baumes gibt es drei grundsätzlich verschiedene Traversierungsstrategien:
- Preorder-Traversierung: Es wird zuerst der Knoten selbst verarbeitet, dann seine Kinder. Das Beispiel oben ist als Preorder-Traversierung geschrieben.
- Postorder-Traversierung: Es werden zuerst die Kinder des Knotens verarbeitet, dann seine Kinder.
- Inorder-Traversierung: Es wird zuerst der linke Kindknoten verarbeitet, dann der Knoten selbst, dann der rechte Kindknoten. Inorder-Traversierung ist nur auf Binärbäume sinnvoll anwendbar.
Hier zum Vergleich die Summen-Funktion mit den beiden anderen Traversierungsstrategien:
|
|
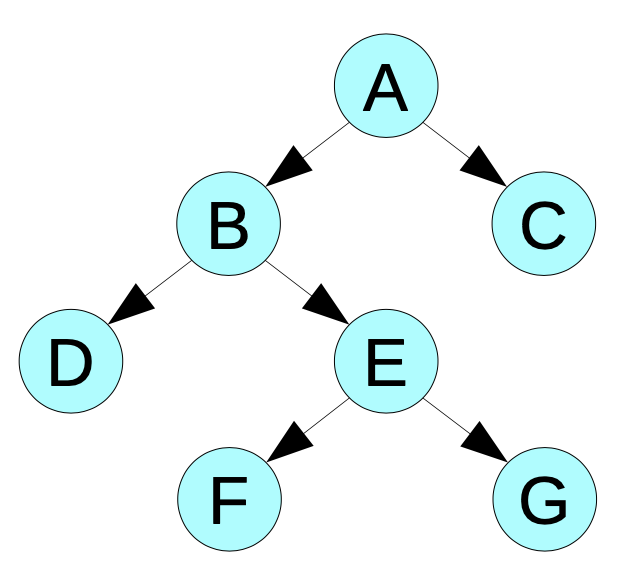
Traversierungsreihenfolgen ZPG Informatik [CC BY-NC-SA 3.0 DE], aus 02_hintergrund_adts.odt
Beispiel für unterschiedliche Traversierungsreihenfolgen:
Preorder-Traversierung: A → B → D → E → F → G → C
Postorder-Traversierung: D → F → G → E → B → C → A
Inorder-Traversierung: D → B → F → E → G → A → C
Beim Aufsummieren spielt es keine Rolle, wie der Baum traversiert wird, weil die Addition (zumindest bei Integer-Werten) kommutativ ist.
Es gibt allerdings verschiedene Situationen, in denen die Traversierungsreihenfolge relevant ist.
Preorder-Traversierung: z.B. Thronfolge in Königshäusern – der älteste Nachkomme des aktuellen Regenten ist direkter Thronfolger, danach dessen ältester Nachkomme usw.
Postorder-Traversierung: z.B. Auswerten von Rechenbaums – zuerst müssen die Ergebnisse der beiden Kinder feststehen, bevor sie mit dem Operator des aktuellen Knotens verarbeitet werden.
Inorder-Traversierung: z.B. lineare Darstellung eines Rechenbaums – zuerst wird der linke Teilbaum ausgegeben, dann das Rechenzeichen des aktuellen Knotens, dann der rechte Teilbaum.
Tiefen- und Breitensuche
Bei den oben beschriebenen Traversierungen geht man „automatisch“ rekursiv vor. Ein solcher Algorithmus führt zu einer Tiefensuche: Es wird zuerst der erste Kindknoten der Wurzel und dann dessen Kindknoten usw. bearbeitet, bevor man zum zweiten Kindknoten der Wurzel kommt. Auf diese Weise wandert man im Baum „zuerst in die Tiefe“, was den Namen „Tiefensuche“ erklärt (im Englischen „depth-first-search“). Wenn man einen Knoten mit einer bestimmten Eigenschaft sucht, wird der am weiten „links“ stehende Knoten gefunden, der die Eigenschaft aufweist.
tiefensuche(b: Binärbaum):
falls b != null UND Attribut(b):
markiere b und Ende
tiefensuche(b.links)
tiefensuche(b.rechts)Man kann dieselbe Abarbeitungsreihenfolge auch mit einem iterativen Algorithmus erreichen. Anstelle eines Rekursionsaufrufs wechselt man bei jedem Schleifendurchlauf zunächst zum ersten Kindknoten. Zudem muss man sich die restlichen Kinder merken, um sie verarbeiten zu können, wenn man mit der Verarbeitung des Teilbaums unterhalb des ersten Kindes fertig ist. Es gilt dabei das „last-in-first-out“-Prinzip, also muss ein Stack verwendet werden.
tiefensucheIterativ(b: Binärbaum):
s = neuer Stack
s.push(b)
solange s nicht leer ist:
k = s.pop()
falls k != null UND Attribut(k)
markiere k und Ende
s.push(b.rechts)
s.push(b.links)Im Codebeispiel wird der rechte Kindknoten vor dem linken Kindknoten auf den Stack gelegt, damit im jeweils nächsten Schleifendurchlauf zuerst der linke Kindknoten verarbeitet wird. Würde man die Reihenfolge umkehren, hätte man ebenso eine Tiefensuche, würde aber den am weitesten rechts stehenden Baumknoten finden.
Unter manchen Umständen ist es notwendig, den Knoten zu finden, der eine bestimmte Eigenschaft hat und am weitesten oben im Baum steht, d.h. dass der Pfad von der Wurzel zum gefundenen Knoten so kurz wie möglich ist18 . Dies lässt sich einfach durch den Austausch der Container-Datenstruktur im obigen Algorithmus erreichen: Anstelle des Stacks nimmt man eine Queue. Der resultierende Algorithmus heißt „Breitensuche“, weil er zuerst „die gesamte Breite“ des Baums durchsucht, bevor er weiter unten weitermacht (englisch „breadth-first-search“).
breitensucheIterativ(b: Binärbaum):
q = neue Queue
q.enqueue(b)
solange q nicht leer ist:
k = q.dequeue()
falls k != null UND Attribut(k)
markiere k und Ende
q.enqueue(b.rechts)
q.enqueue(b.links)Auf diese Weise wird der Baum „Schicht für Schicht“ abgearbeitet: Zuerst die Wurzel, dann die direkten Kinder, dann deren Kinder usw.19
Es fällt auf, dass die beiden Algorithmen strukturell sehr ähnlich sind. Wenn man Stack und Queue in einer gemeinsamen Oberklasse zusammengefasst hat (vgl. Seite 11), kann man Tiefen- und Breitensuche in eine gemeinsame Funktion zusammenfassen:
tiefenBreitenSuche(b: Binärbaum, c: Container):
c.insert(b)
solange c nicht leer ist:
k = c.removeNext()
falls k != null UND Attribut(k)
markiere k und Ende
q.insert(b.rechts)
q.insert(b.links)tiefensuche(b: Binärbaum):
tiefenBreitenSuche(b, neuer Stack)breitensuche(b: Binärbaum):
tiefenBreitenSuche(b, neue Queue)
16 Bei Verzeichnisbäumen ist ein solches Vorgehen z.B. sinnvoll.
17 Die Datenstruktur Baum ist eine mögliche Implementation des ADTs Baum, so wie die Datenstruktur „verkettete Liste“ eine mögliche Implementation des ADTs Liste ist.
18 Da in einem Baum der Pfad von der Wurzel zu einem Knoten immer eindeutig ist, führen Tiefen- und Breitensuche auf Bäumen stets zum gleichen Ergebnis, wenn nur ein Knoten das Suchattribut erfüllt. Für allgemeine Graphen ist der Unterschied hingegen deutlich relevanter.
19 Bei der Breitensuche wird zuerst der rechte, dann der linke Kindknoten eingereiht. Damit wird jede Schicht „von rechts nach links“ verarbeitet. Bei der Tiefensuche wird aber zuerst der linke, dann der rechte Kindknoten verarbeitet. Dies ist nützlich, um später Tiefen- und Breitensuche zu vereinheitlichen.
Hintergrundinformationen: Herunterladen [odt][305 KB]
Weiter zu Rekursion
