Kellerautomaten (neu im BP: Item 13)
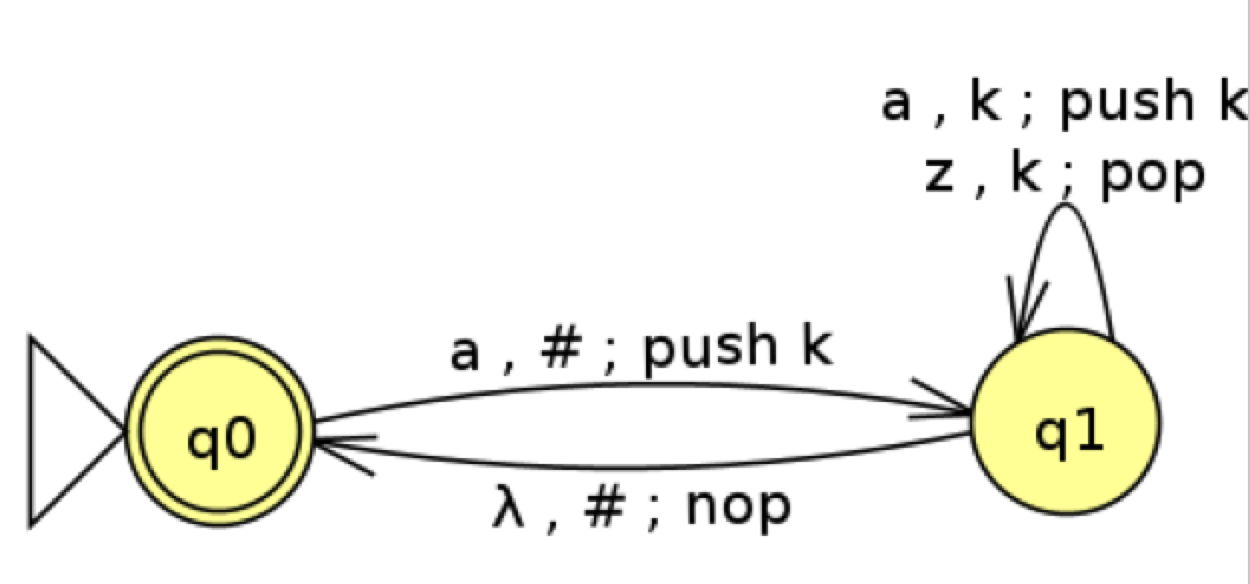
Abbildung 5: Stackautomat für die Erkennung von Klammerpaaren ohne Inhalt; a steht für "Klammer auf" und z für "zu"; das Zeichen # für einen leeren Stack. Achtung: Die Skizze verwendet die besser lesbare Syntax (#, push, pop), die JFLAP aber nicht ausführen kann! ZPG Informatik [CC BY-SA 4.0 DE], aus zpg_sprachenautomaten_hintergrund.odt
Ein Kellerautomat16 ist ein normaler DEA, der neben seinen Zuständen und Übergängen auch einen Kellerspeicher, also einen LIFO-(last in, first out) Speicher besitzt. Der Kellerautomat kann
- jede Transition zusätzlich vom obersten Element des Stack abhängig machen und
- bei jeder Transition auch den Stack manipulieren, also einen zusätzlichen Wert darauflegen (PUSH17 ), den obersten Wert entnehmen (POP) oder den Stack unverändert lassen (NOP).
Der entscheidende Unterschied zum DEA ist hier der unbegrenzte Speicherplatz auf dem Stack.
Während DEAs Klammersprachen nicht erkennen können, ist anschaulich klar, wie ein Kellerautomat dieses Problem löst: Er beginnt mit leerem Stack und legt bei jeder öffnenden Klammer ein Symbol (z.B. „k“ für Klammer) darauf ab. Bei jeder schließenden Klammer entfernt er eines; die Anzahl der „k“ auf dem Stack zählt also die momentane Klammerungstiefe; das Entfernen vom leeren Stack führt zu einem Fehler. Der Automat für diese Aufgabe muss in einem Endzustand stehen (und das Wort damit akzeptieren), falls am Ende der Eingabe auch der Stack leer ist.
Bild 5 zeigt einen einfachen Kellerautomaten, der Klammerausdrücke erkennt. Vom Input werden hier nur die Klammern selbst betrachtet und ihr „Inhalt“ ignoriert; zugunsten der Lesbarkeit verwenden wir außerdem a und z statt „Klammer-auf“ und „-zu“. Korrekt geklammerte Ausdrücke sind also etwa az, aaazzz, azaz oder aazazz. Wie schon angesprochen gilt auch das leere Wort als korrekt geklammert.
Im Übergangsgraphen bedeutet die Transition (a, k; push k) Folgendes: „FALLS im Zustand q1 das Eingabezeichen a anliegt UND auf dem Stack ein k liegt, DANN wechsle in Zustand q1 und push ein weiteres k“. Das Zeichen # steht für einen leeren Stack, das λ für „kein Eingabezeichen“ (Merkhilfe: lambda für „leer“, oft auch epsilon für „empty“). Diese Transition verbraucht also keine Eingabe.
Um Kellerautomaten im Unterricht ausführlicher zu behandeln, muss man eine übersichtliche Darstellung für deren Beschreibung wählen, denn ihre Transitionstabelle ist (anders als die eines DEA) leider dreidimensional, da die Übergänge a) vom aktuellen Zustand, b) vom Eingabezeichen und c) auch noch vom Zeichen auf dem Stack abhängen. Obendrein enthält jede Transition den Nachfolgezustand und eine Stackoperation. Auch ein „Lauf“ des Automaten ist aufwändiger zu protokollieren als bei einem DEA (siehe Seite 12).
Hinweis zu Item 13 des Bildungsplans
Der Bildungsplan Abschnitt „3.3.5 Automaten und formale Sprachen“ enthält in Item 13 die Formulierung „kontextfreie Sprachen durch Kellerautomaten und kontextfreie Grammatiken beschreiben“. Sie ist so zu verstehen, dass Schülerinnen
- kontextfreie Sprachen durch kontextfreie Grammatiken beschreiben
- und damit auch Herleitungen durchführen (also Wortprobleme lösen) können.
Kellerautomaten werden nur als Erweiterung von DEA behandelt, weil sie auch kontextfreie Sprachen erkennen können. Man muss daher...
- die prinzipielle Arbeitsweise eines Kellerautomaten bei der Erkennung einer gegebenen Sprache beschreiben können,
- die Beschreibung eines Kellerautomaten (der als Zustandsübergangsdiagramm oder in einer formalen Darstellung gegeben ist) interpretieren und erläutern sowie einen Lauf dieses Automaten protokollieren können, …
Formale Darstellung eines Kellerautomaten
Eine formale und vollständige Beschreibung des Kellerautomaten aus Abbildung 5 umfasst...
| … allgemein: | … im Beispiel: |
| das Eingabealphabet ∑ | ∑ = {a, z} |
| eine Menge Z von Zuständen | Q = {q0,q1,qF} (incl. Fehlerzustand!) |
| den Startzustand s ∈ Z | s = q0 |
| eine Menge E ⊆ Z von Endzuständen | E = {q0} |
| das Stackalphabet Γ (Gamma) | Γ ={#, k}; das # steht für einen leeren Stack |
| Kriterien | Auswirkung | ||||
| alter Zustand? | Eingabe? | auf Stack? | → | neuer Zustand | Operation |
| 0 | a | # | → | 1 | push k |
| 1 | a | k | → | 1 | push k |
| 1 | z | k | → | 1 | pop k |
| 1 | λ | # | → | 0 | nop |
Ablaufprotokoll eines Kellerautomaten
Ähnlich wie ein Schreibtischtest den Ablauf eines Programms dokumentiert, kann auch der „Lauf“ eines Kellerautomaten dokumentiert werden, wobei die durchlaufenen Zustände, die Entwicklung des Stack und das Verbrauchen der Eingabe sichtbar werden sollten. Dazu eignet sich beispielsweise die Darstellung wie in Tabelle 1.
Tabelle 1: Ablaufprotokoll des Kellerautomaten aus Abbildung 5 für die Eingabe aazazz
| Stack ↑ | |||||||||
| k | k | ||||||||
| k | k | k | k | k | |||||
| # | # | # | # | # | # | # | # | ||
| Zustand | q0 | q1 | q1 | q1 | q1 | q1 | q1 | q0 | |
| Vom Übergang verbrauchtes Eingabezeichen | a | a | z | a | a | z | Eingabe endet, q0 ist Endzustand: Wort wird akzeptiert! | ||
Die angedeuteten Koordinatenachsen spannen dabei nach oben die Höhe des Stapels, nach rechts die Zeit auf; im Diagramm sieht man, wie er mehrfach wächst und schrumpft. Unter der Rechtsachse wird der jeweils erreichte Zustand notiert und in der letzten Zeile das Eingabezeichen, das der jeweilige Zustandsübergang verbraucht hat.
Aufmerksame Schüler könnten bemerken, dass die Eingabe endet, während der Automat noch in Zustand q1 steht – also nicht in einem Endzustand! Trotzdem akzeptiert er die Eingabe, weil der letzte Übergang (von q1 nach q0) ohne Vorliegen oder Verbrauchen eines Eingabezeichens stattfindet. Dieser Übergang mutet insofern „etwas nichtdeterministisch“ an. Dennoch wird ein solcher Automat als deterministisch bezeichnet18 , sofern zwischen den Transitionen mit Eingabezeichen (zweite und dritte Zeile der Übergangstabelle, Eingabe a bzw. z) und denen mit λ (vierte Zeile) keine Mehrdeutigkeiten auftreten.
Was Kellerautomaten können (BP: Item 14)
Wie in der Tabelle auf Seite 3 schon beschrieben , erkennen Kellerautomaten genau die kontextfreien Sprachen. Zwar werden diese ebenso durch kontextfreie Grammatiken oder Syntaxdiagramme beschrieben; für die Klärung, welche Sprachen denn kontextfrei sind und welche nicht, könnte man also auch letztere heranziehen. Die Anschauung eines Stapels und wie der Automat ihn während der Erkennung sukzessive auf- und abbaut, ist aber besser nachvollziehbar, weswegen wir für schon für die Klammersprachen damit argumentiert haben.
| Sprache | kann von PDA erkannt werden | Begründung |
| L = {an zn : n∈ℕ} | ja | ist ein Spezialfall der Klammersprache |
| L = {an bm cn : m, n∈ℕ} | ja | Stack wird mit den a beladen, dann alle b lesen (Anzahl unerheblich), dann Stack über die c wieder entladen |
| L = {ak bm cn : k, m, n∈ℕ} | ja | Diese Sprache kann sogar von einem DEA erkannt werden (die Anzahlen der a, b und c müssen ja gar nicht übereinstimmen, so dass der Automat sie auch nicht zählen muss), also erst recht von einem Kellerautomaten. |
| L = {an bn cn : n∈ℕ} | nein | Der Automat müsste die a einlesen und dabei den Stack beladen. Für die Zählung der b muss er ihn anschließend wieder entladen (denn nur auf diese Weise kann er zählen). Danach ist der Stack leer, er hat die Anzahl „vergessen“ und kann daher die c nicht mehr zählen. Mit zwei Stacks würde es allerdings gehen. |
| L = Menge aller Vornamen der deutschen Sprache | ja | Diese Sprache enthält sowieso nur endlich viele Wörter. Damit kann sie sogar von einem DFA erkannt werden, also erst recht von einem Kellerautomaten. |
| XML-artige Sprachen mit vorher festgelegten Tags | ja | (siehe Abbildung 6) |
| allgemeines XML | nein | (siehe Abbildung 6) |
| Java | nein | (siehe unten) |

Abbildung 6: Prinzipskizze eines XML-Dokuments mit geschachtelten Tags ZPG Informatik [CC BY-SA 4.0 DE], aus zpg_sprachenautomaten_hintergrund.odt
Das Beispiel in Abbildung 6 zeigt, dass bei XML-artigen Sprachen die öffnenden <...> und schließenden </...> Tags eine klammerartig geschachtelte Struktur bilden. Falls die erlaubten Tags von vornherein festgelegt sind (in HTML z.B. <table>, <p>, <title> usw.), kann man für die Erkennung eine Kellermaschine konstruieren: Ihr Stapelalphabet Γ muss dann für jedes bekannte Tag einen „Tag-Code“ enthalten, der bei Auftreten dieses Tags auf den Stack gelegt wird. Anhand der schließenden Tags in der Eingabe kann der Automat den Stack dann passend wieder abbauen und dabei überprüfen, ob das in der Eingabe gerade geschlossene Tag auch das ist, das zuletzt auf dem Stapel gespeichert worden war.
Falls die erlaubten Tags hingegen nicht im Voraus festgelegt sind (und bei allgemeinem XML sind sie eben nicht festgelegt), ist die Situation schwieriger: Weil das Stackalphabet nicht passend erweitert werden kann, könnte der Automat die öffnenden Tags allenfalls zeichenweise auf den Stack legen. Wenn er dann aber ein schließendes Tag antrifft und dessen Zeichen (vorwärts!) aus der Eingabe liest, kann er sie nicht mit dem Tag abgleichen, dessen Zeichen nur rückwärts vom Stack gelesen werden können. Wie schon bei DEA kann auch dieses Problem wieder nicht durch eine endliche Zahl zusätzlicher Zustände gelöst werden, wenn die Tags beliebig lang sein dürfen.
Auch Java oder ähnliche Programmiersprachen kann eine Stackmaschine nicht erkennen. Für die Begründung argumentiert man allerdings nicht mit dem Stack, sondern ausnahmsweise mit der zugehörigen kontextfreien Grammatik (ab Seite 19): Man betrachtet ein Fragment wie
1 public void fehlerhaft() {
2 int k = 12;
3 m = k + 1;
4 }
16 Ein Keller wird oft Stapel oder (auch im Deutschen) Stack genannt, für Kellerautomaten sind „Stackautomat“ oder PDA („pushdown automaton“) gebräuchlich.
17 Hinweis: Hier wurde eine übersichtlichere Schreibweise mit PUSH, POP und NOP verwendet, die aber zu JFLAP nicht kompatibel ist. JFLAP erlaubt es (leider) sogar, das Zeichen # noch vom leeren Stack zu POPen, der anschließend „ganz leer“ ist. Da sie für die Erfüllung des Bildungsplans nicht erforderlich ist, empfehlen wir, auf die praktische Arbeit mit PDAs in JFLAP zu verzichten.
18 Quelle z.B. https://de.wikipedia.org/wiki/Kellerautomat#Formale_Definition “Wenn die Übergangsfunktion die Eigenschaft ∀ z∈Z , ∀ a∈Σ , ∀ g∈Γ , | δ ( z , a , g ) | + | δ ( z , ε , g ) | ≤ 1 erfüllt, spricht man von einem deterministischen Kellerautomaten. Zu einer festen Eingabe gibt es dann höchstens eine Zustandsübergangsabfolge, Mehrdeutigkeiten können also nicht auftreten.“
Hintergrundinformationen: Herunterladen [odt][669 KB]
Weiter zu Turingmaschinen
