Verknüpfung binärer Datenworte
Logische Verknüpfungen
Wir wollen uns nun den Verknüpfungen binärer Daten zuwenden. Die logischen Verknüpfungen ganzer Datenworte stellen dabei kein großes Problem dar: Jedes der einander entsprechenden Bits der zwei (gleichgroßen!) Datenworte wird einfach durch ein passendes Gatter miteinander verknüpft.
Addition binärer Zahlen
Der Algorithmus der Addition von Binärzahlen ist durch das Verfahren der schriftlichen Addition gegeben: wir müssen also den Algorithmus der schriftlichen Addition „in Elektronik“ übersetzen. Betrachten wir zunächst ein Rechenbeispiel mit zwei 4-stelligen Datenworten (wobei die niederwertigste Stelle (also das „LSB“) ganz rechts steht):
| 0 | 1 | 1 | 0 | |
| + | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 |
Welche elementaren Aufgaben müssen hierfür gelöst werden? Folgende Additionen können an der niederwertigsten Stelle auftreten:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Die ersten 3 Zeilen stellen kein Problem dar: solange das Ergebnis der Elementar-Addition einstellig ist, ist die Welt in Ordnung. Schwieriger wird es in der vierten Zeile: dort liegt ein zweistelliges Ergebnis vor, was einen Übertrag 1 in die nächst-höherwertige Stelle zur Folge hat. Bei den ersten drei Rechnungen hat der Übertrag hingegen stets den Wert 0. Zur Bewältigung der Addition zweier einstelliger Binärzahlen brauchen wir also eine Schaltung mit 2 Eingängen A und B sowie zwei Ausgängen S (für den Stellenwert) und C (Carry, englisch für den Übertrag). Diese Schaltung muss die folgende Wahrheitswert-Tabelle haben:
| a | c | cout | s |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Diese Schaltung nennt man einen Halbaddierer und stellt sie durch das folgende Symbol dar:

Symbol Halbaddierer
Das folgende Bild zeigt eine Implementierung eines Halbaddierers. Es gibt allerdings auch Implementierungen, die mit weniger Transistoren auskommen:

Halbaddierer
Warum ist dies nur ein „Halb“-Addierer? Die zurückhaltende Bezeichnung ist darauf zurückzuführen, dass die Schaltung zwar den Übertrag auf der Ausgangsseite korrekt produzieren kann, aber keinen Eingang für einen eventuell von einer niederwertigeren Stelle gelieferten Übertrag hat. Studiert man nochmals den Algorithmus der schriftlichen Addition, dann fällt auf, dass für jede Stelle (außer der niederwertigsten) wegen des möglichen Übertrags der vorherigen Stelle die Addition von eigentlich 3(!) einstelligen Binärwerten ermöglicht werden muss.
Analog zum obigen Vorgehen könnte man nun die Wahrheitswert-Tabelle eines Volladdierers mit 3 Eingängen aufstellen und versuchen, eine entsprechende Schaltung zu entwerfen. Dies ist eine lohnende Hausaufgabe für ambitionierte Schüler. Allerdings ist sowohl die erfolgreiche Bearbeitung der Aufgabe als auch eine eventuelle Überprüfung und Korrektur der erarbeiteten Lösungen recht mühsam.
Der Ansatz, aus der Wahrheitswerttabelle die Schaltung zu entwickeln, erinnert an die „Brute-Force-Methode“. Geschickter ist hier die Anwendung eines „Divide-and-Conquer“-Ansatzes: man zerlege das Problem in kleinere Einzelprobleme, löse diese und versuche dann, die Lösung des ursprünglichen Problems aus den Einzellösungen zusammenzusetzen. Zumindest die Zerlegung geht im vorliegenden Fall sehr einfach: statt eine Addition dreier Bits „in einem Rutsch“ zu betrachten, nehmen wir zuerst mal zwei der Bits und addieren diese. Dann addieren wir zum Zwischenergebnis das dritte Eingangsbit. Eigentlich müssen wir also nur zwei Halbaddierer hinter einander schalten:
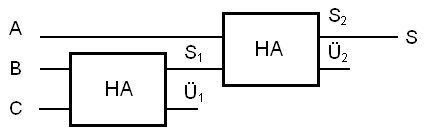
Addition von drei Bits
Der Ausgang S enthält offensichtlich den Stellenwert des Ergebnisses. Aber welcher der beiden Überträge Ü1 und Ü2 ist der richtige? Nun, da ein Übertrag bei der ersten oder auch bei der zweiten Addition auftreten könnte, müssen irgendwie beide Überträge berücksichtigt werden.
Die komplette Volladdierer-Schaltung wird mit dem folgenden Symbol abgekürzt:
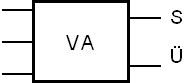
Volladdierer
Eine Schaltung zur Addition zweier 4-Bit-Binärzahlen könnte dann entsprechend so aussehen:
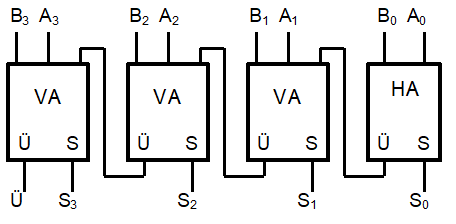
Carry-Ripple-Addierer
Achtung! Die Addition zweier 4-Bit-Zahlen kann eine 5-Bit-Zahl ergeben. Für das Abspeichern der vollständigen Summe ist also eine größere Wortbreite nötig als für die Summanden! Dieses Problem taucht bei sämtlichen numerischen Datentypen auf und muss entsprechend in allen Berechnungsalgorithmen berücksichtigt werden.
Subtraktion binärer Zahlen
Bisher haben wir die verwendeten 4-Bit-Worte bei der Interpretation als Zahlen stets als natürliche Zahlen angesehen. Gemäß der folgenden Tabelle lässt sich also mit einem solchen 4-Bit-Wort ein Zahlenbereich von 0..15 beschreiben:
| Bits | Zahl |
|---|---|
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| Bits | Zahl |
|---|---|
| 1000 | 8 |
| 1001 | 9 |
| 1010 | 10 |
| 1011 | 11 |
| 1100 | 12 |
| 1101 | 13 |
| 1110 | 14 |
| 1111 | 15 |
Addiert man zu 1111b = 15 nun nochmals eine 1, dann erhält man 10000b = 16, was aber 5 Bits zur Speicherung braucht und daher nicht mehr in ein 4-Bit-Wort passt. Schreibt man dieses Ergebnis dann eben „soweit es geht“ stellengerecht in einen 4-Bit-Speicher, dann erhält man als Resultat dieser Addition das Bitmuster „0000“. Mithin erscheint der Zahlenraum zyklisch geschlossen:

zyklische Anordnung
In einer solchen zyklischen Anordnung ist die Interpretation der Bitmuster als rein positive ganze Zahlen nicht mehr zwingend. Man könnte auch eine Hälfte der Zahlen als positive und die andere Hälfte als negative Zahlen ansehen. Da in der Menge der ganzen Zahlen die 0 den Vorgänger -1 hat, müsste dieser Zahl das Bitmuster „1111“ entsprechen, der -2 das Muster „1110“. Üblicherweise wird das höchstwertige Bit als Vorzeichen-Indikator genommen: alle Bitmuster der Form „1xxx“ werden als negativ interpretiert, alle der Form „0xxx“ als positiv. Die sich damit ergebende Zuordnung ist im folgenden Diagramm durch den zusätzlichen inneren Zahlenkreis dargestellt:

Zweier-Komplement-Darstellung
So lässt sich der Zahlenraum von -8 bis +7 mit 4-Bit-Worten darstellen. Man nennt die hier gewählte Darstellung der negativen Zahlen die Zweier-Komplement-Darstellung.
Was uns noch fehlt, ist ein Algorithmus, mit dem wir aus dem Bitmuster für eine Zahl a > 0 das Bitmuster der Zahl (‑a) erhalten können. Schauen wir uns dazu mal ein Beispiel an:
Die Zahl 3 hat das Bitmuster „0011“. Wenn wir nun dieses Muster bitweise invertieren (also jede 0 durch eine 1 ersetzen und jede 1 durch eine 0), dann erhalten wir das Muster „1100“. Ein Blick in die obige Tabelle zeigt, dass wir dicht neben dem richtigen Ergebnis landen, nämlich bei (-4). Wenn wir nun zu dieser Zahl noch eine 1 addieren, dann erhalten wir das korrekte Bitmuster „1101“ für (-3). Allgemein gilt der folgende Algorithmus zur Bildung des Zweierkomplements einer Zahl a:
Man invertiere das Bitmuster von a und addiere zum Ergebnis eine 1.
Wenn wir das bitweise Inverse einer Zahl a mit a bezeichnen und das Zweier-Komplement von a mit a*, dann lässt sich die obige Regel als Formel schreiben:
a* = a + 1
Um den Nutzen der Zweierkomplement-Darstellung für negative Zahlen einzusehen, klären wir zunächst, wie man die Bildung des Zweierkomplements einer Zahl a mathematisch beschreiben kann. Liegt a in einer Darstellung mit N Bits vor, dann kann man das bitweise Inverse von a, also a, erhalten, indem man a von einer Binärzahl abzieht, die aus genau N Einsen besteht. Im obigen konkreten Beispiel wäre also zu rechnen: „1111“ - „0011“ = „1100“, wobei die Differenz in Zahlen geschrieben bedeutet: (24 – 1) – 3. Die Zweierkomplement-Darstellung erhält man nun, indem man zu diesem Term noch eine 1 addiert: (24 – 1) – 3 + 1 = 24 – 3. Allgemein ergibt sich für das Zweier-Komplement a* einer positiven Zahl a in N-stelliger Binärdarstellung der Term
a* = 2N – a.
Damit lässt sich eine Subtraktion zweier positiver Zahlen stets folgendermaßen realisieren:
b – a = b – a + 2N – 2N = b + 2N – a – 2N = b + (2N – a) – 2N = b + a* – 2N
Zur Ausführung der Subtraktion b - a kann also ein normales Addierwerk verwendet werden, wenn man an dessen Eingänge den Minuenden b und die Zweierkomplement-Darstellung a* des Subtrahenden anlegt und vom Ergebnis schließlich noch 2N abzieht. Die Subtraktion von 2N schließlich können wir einfach realisieren, indem wir ein eventuell gesetztes Übertrags-Bit in der höchstwertigen Stelle des Ergebnisses ignorieren: da dieses zusätzliche Bit ohnehin beim Abspeichern in einem N-Bit-Datenwort keinen Platz hat, lässt man es einfach unberücksichtigt.
Das Problem der Subtraktion wird also vollständig durch die Zweier-Komplement-Kodierung der negativen ganzen Zahlen gelöst, und zwar gemäß der Umformung:
b – a = b + (-a)
die wir ja aus der Mathematik kennen. Für uns sieht diese Gleichung nun (bei Beschränkung auf N Binärstellen!) so aus:
b – a = b + a*.
Probleme beim Rechnen mit beschränkter Stellenzahl
Damit sind noch nicht alle Probleme der binären Addition bzw. Subtraktion gelöst. Das berechnete Ergebnis EB stimmt nämlich nur dann mit dem korrekten Ergebnis E überein, wenn letzteres(!) innerhalb des zulässigen Zahlbereichs (hier: [‑8;+7]) liegt. Das berechnete Ergebnis EB liegt scheinbar immer in diesem Zahlbereich, was schon durch die Hardware des Addierers gesichert ist! Für unsere 4-Bit-Zahlen ist z.B. schon die Addition 6 + 3 eine unüberwindliche Hürde, denn sie liefert Ü = 0 und das Bitmuster S = 1001, und damit EB = (-7)! Solch ein „Überlauf“ sollte durch geeignete Maßnahmen erkannt werden, so dass dann die Software zumindest melden kann, dass die Berechnung fehlgeschlagen ist. Allerdings ist die Erkennung nicht einfach zu implementieren. Das hier angegebene Beispiel lehrt schon, dass die Überwachung des Ü-Ausgangs der Rechenschaltung keinesfalls genügt, und dass „Übertrag“ und „Überlauf“ zwei total verschiedene Dinge sind!
Das Überlaufproblem ist ein grundsätzliches Problem der Computerarithmetik, weil alle numerischen Datentypen fester Größe eben stets nur endlich viele verschiedene Werte annehmen können. Mithin gibt es stets eine größte und eine kleinste darstellbare Zahl. Überschreiten die korrekten Ergebnisse einer Aufgabe die dadurch gesetzten Grenzen, können die Berechnungsalgorithmen sinnlose Werte liefern. Um dies zu vermeiden, kann man sich numerischer Datentypen bedienen, die nicht mit einer festen Stellenzahl arbeiten. So gibt es z.B. in JAVA zur Darstellung großer Zahlen die dynamischen Datentypen BigInteger und BigDezimal, welche das Rechnen mit beliebig vielen Stellen erlauben. Der Umgang damit ist aber nicht ganz einfach, und die Performance solcher Programme kann problematisch sein. So wird man sich in den meisten Fällen doch der endlichen Standard-Datentypen bedienen.
Viele Compiler verzichten aus Performance-Gründen zumindest bei der Integer-Arithmetik auf jegliche Überlauferkennung (z.B. die Pascal-Compiler der Delphi-Serie). So bleibt es dem Programmierer der Software anheimgestellt, seine Programme selbst gegen Überläufe zu sichern. Lässt man dabei nicht die gebotene Sorgfalt walten, kann das durchaus schlimme Folgen haben. Ein Überlauf war z.B. 1996 der Grund dafür, dass die Ariane5-Rakete auf ihrem Jungfernflug abstürzte. Im Navigationssystem der Rakete wurde vor dem Start eine 64-Bit-Float-Zahl gerundet und der gerundete Wert in eine 16-Bit-Integer-Zahl geschrieben. Leider ergab sich beim Runden ein Wert, der mehr als 16 Bits groß war, weshalb einige der höherwertigen Bits beim Speichern verloren gingen. Der falsche gespeicherte Wert führte dann bei weiteren Berechnungen zum Absturz des Navigationssystems der Rakete. Der damit orientierungslos gewordene Hauptcomputer der Rakete änderte die Flugbahn danach eigenmächtig so stark ab, dass die Bodenstation die Selbstzerstörung der Rakete einleiten musste.
Hintergrundinformationen: Herunterladen [odt][4 MB]
Weiter zu Registermaschine
