Vorbereitung

1. Rationale Zahlen liegen dicht
   Zwischen zwei beliebigen Brüchen gibt es unendlich viele weitere Brüche 
   (Klasse 6 und Wiederholung in Klasse 8).
   Dies ist durch fortgesetztes Erweitern leicht einsichtig zu machen, in seiner Aussage aber gewaltig. Analog lässt sich auch leicht erläutern, dass zwischen zwei abbrechenden Dezimalzahlen (wie 2,516 und 2,517) unendlich viele Zahlen liegen.
2. Brüche stellen zwei Arten von Dezimalzahlen dar
   Brüche stellen entweder abbrechende oder periodische Dezimalzahlen dar
   (Klasse 6 und Wiederholung in Klasse 8).
   Es ist sinnvoll, schon früh die Brüche als Dezimalzahlen darzustellen und diese Darstellung durch händische Division herzustellen. Die Einsicht in die beiden möglichen Darstellungen erfolgt automatisch. Die Frage nach der Bruch-Struktur abbrechender Dezimalzahlen vertieft die Einsichten in Teiler und Stellenwerte.
3. Außer Brüchen gibt es weitere Dezimalzahlen
   Es gibt weitere Dezimalzahlen, die weder abbrechend noch periodisch sind, also nicht als Brüche dargestellt werden können.
   Hier sollte man spielerisch neue Dezimalzahlen erkennen und entdecken lassen. Dabei sollte altersgemäß immer wieder darauf verwiesen werden, dass sich bereits „sehr, sehr viele“ Bruchzahlen auf dem Zahlenstrahl drängen.

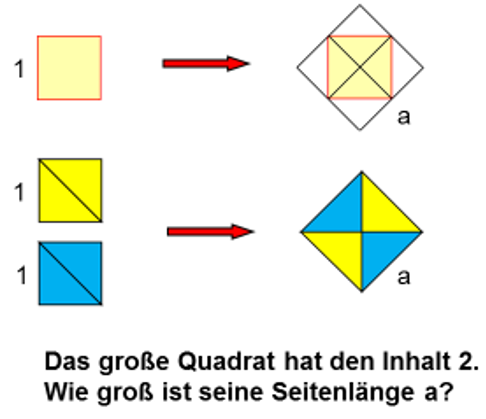
Zugang: Quadratverdoppelung

 

Artikel: Herunterladen [pdf][1 MB]

Weiter zu Näherungsverfahren