Lösungen

Zum Einstieg

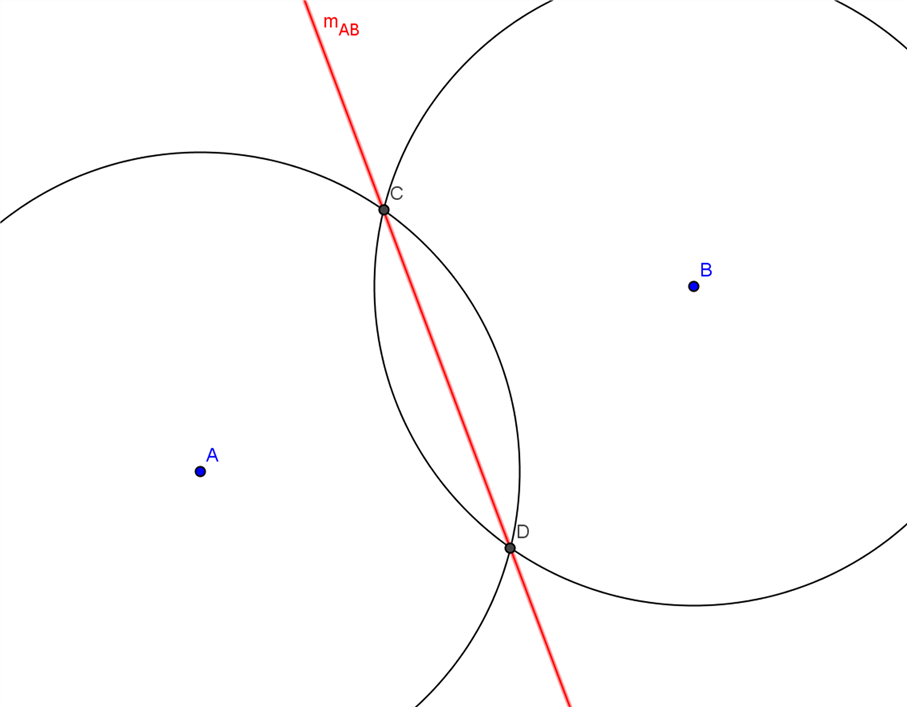
Mittelsenkrechte

1. Zeichne einen Kreis um A mit einem Radius r, der größer ist, als die Länge der halben Strecke AB.
2. Zeichne einen Kreis um B mit dem gleichen Radius.
3. Die Gerade durch die beiden Schnittpunkte der Kreise ist die Mittelsenkrechte m_AB.

 

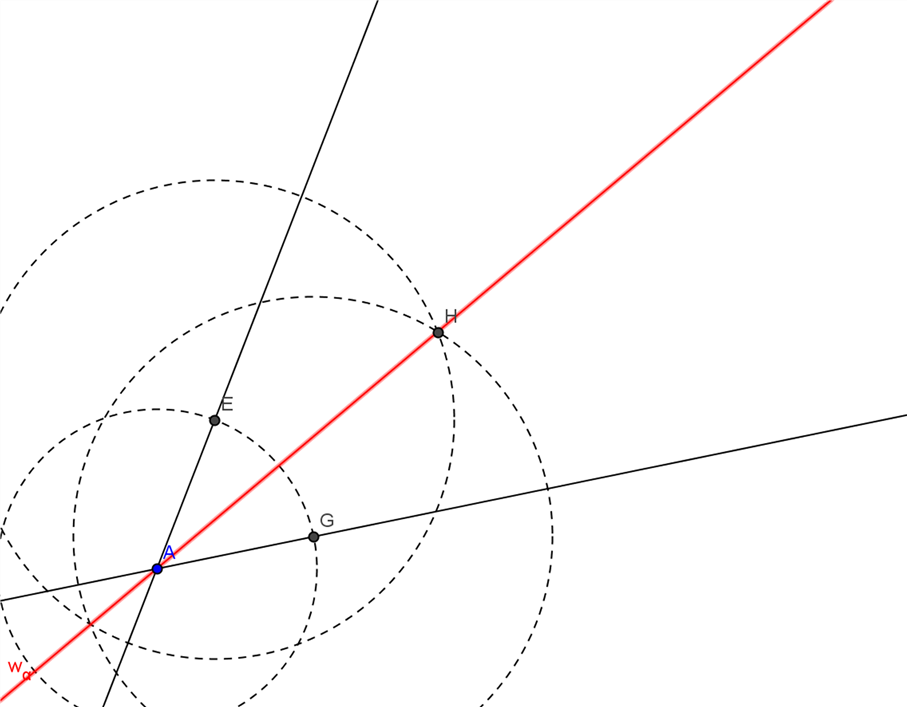
Winkelhalbierende

1. Zeichne einen Kreis um den Schnittpunkt der Geraden.
2. Der Kreis schneidet die Geraden auf der einen Seite in zwei Punkten (hier: E und G). Zeichne um beide einen Kreis mit gleichem Radius.
3. Die Gerade durch den Punkt A und den Schnittpunkt H der beiden Kreise ist die Winkelhalbierende w_a.

Bemerkung: bei Geraden gibt es noch eine weitere Winkelhalbierende durch den Nebenwinkel von a.

 

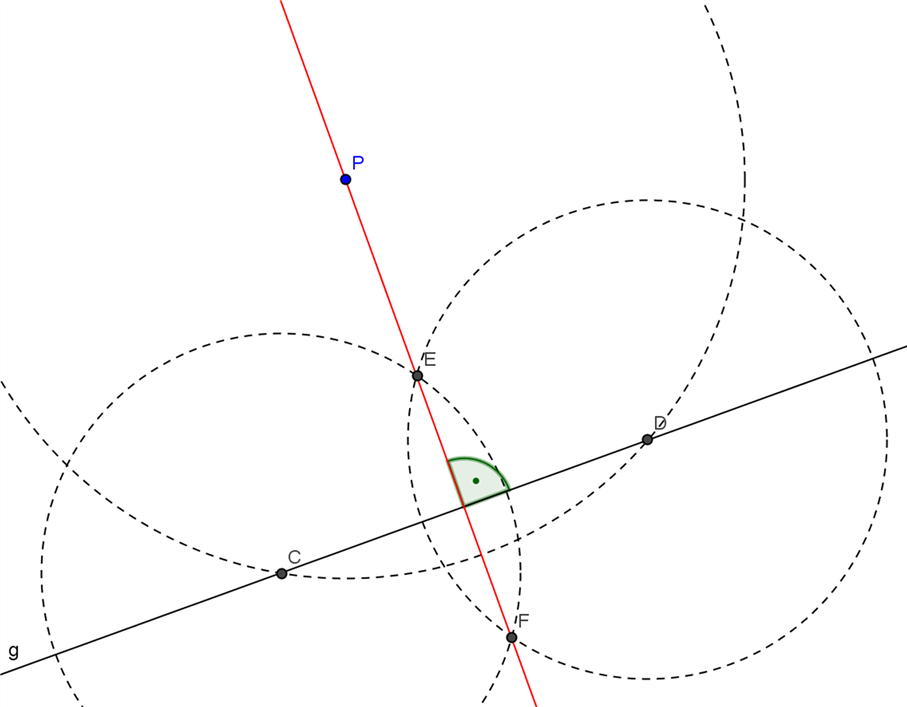
Orthogonale zu einer Geraden g durch einen Punkt P

1. Zeichne Kreis mit Mittelpunkt P und Radius so, dass der Kreis die Gerade zweimal schneidet.
2. Die Mittelsenkrechte zu den beiden Schnittpunkten ist die Orthogonale zu g durch P.

Auftrag 1

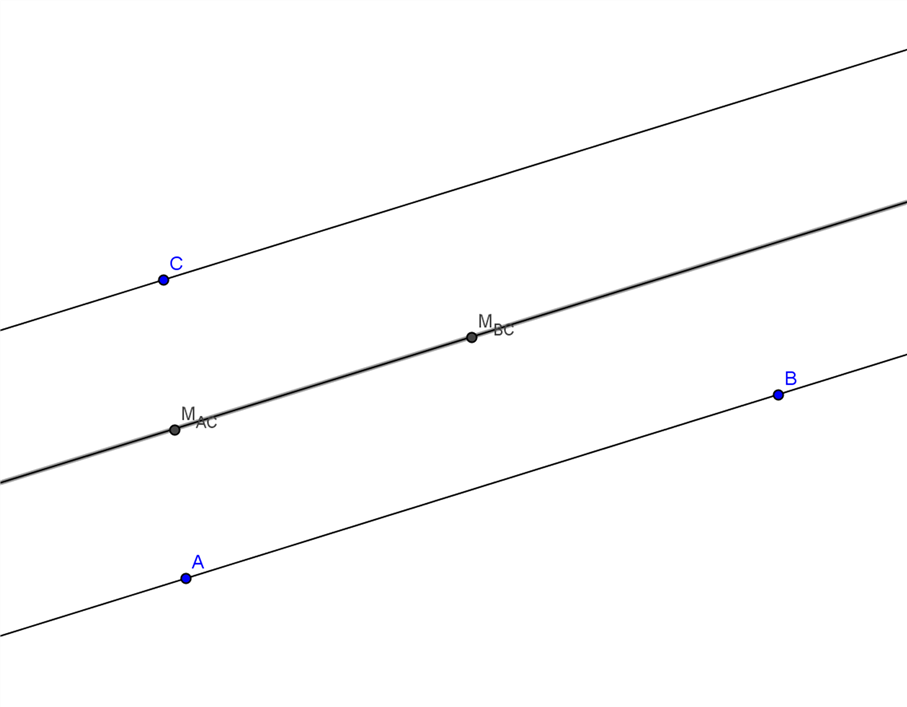
Konstruktion der Mittelparallelen

1. Konstruiere den Mittelpunkt von A und C. (Wie bei Mittelsenkrechter)
2. Konstruiere den Mittelpunkt von B und C.
3. Verbinde die beiden Punkte durch eine Gerade. Diese ist die Mittelparallele.

 

Auftrag 2

a) Gesucht wird ein Punkt, der von drei vorgegebenen Punkten P, Q und R gleich weit entfernt ist.

b)

 

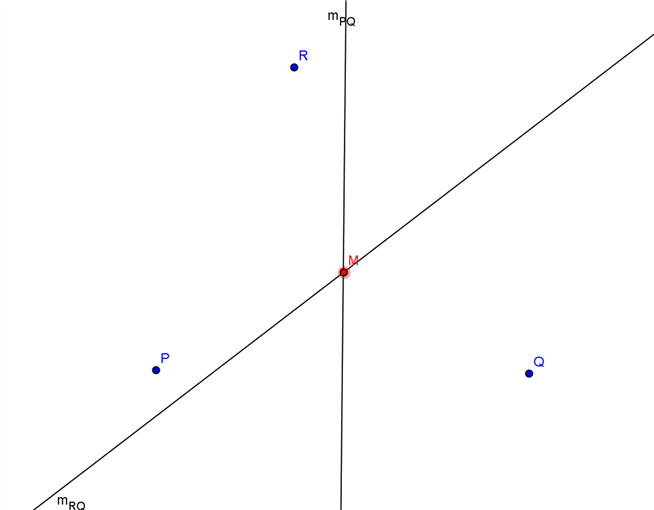
Konstruiere zu zwei der Strecken PQ, QR und PR die Mittelsenkrechte. Der Schnittpunkt ist der gesuchte Punkt.

c) Konstruktion des Mittelpunktes eines Kreises

Wähle drei beliebige Punkte auf dem Kreis und verfahre wie in a)

 

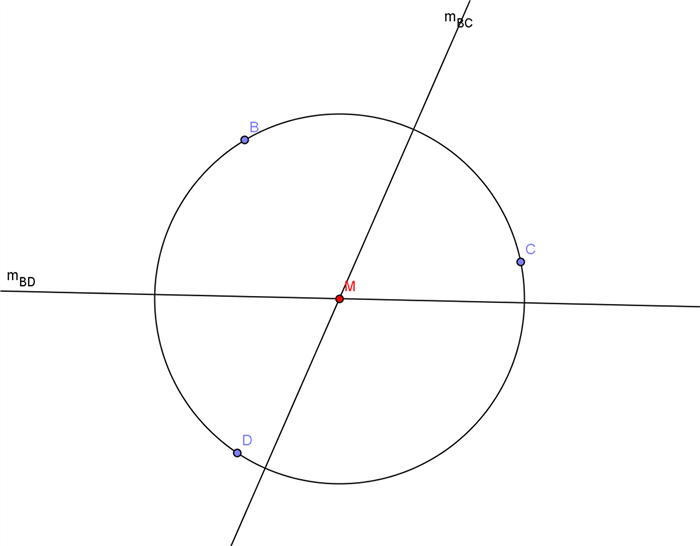
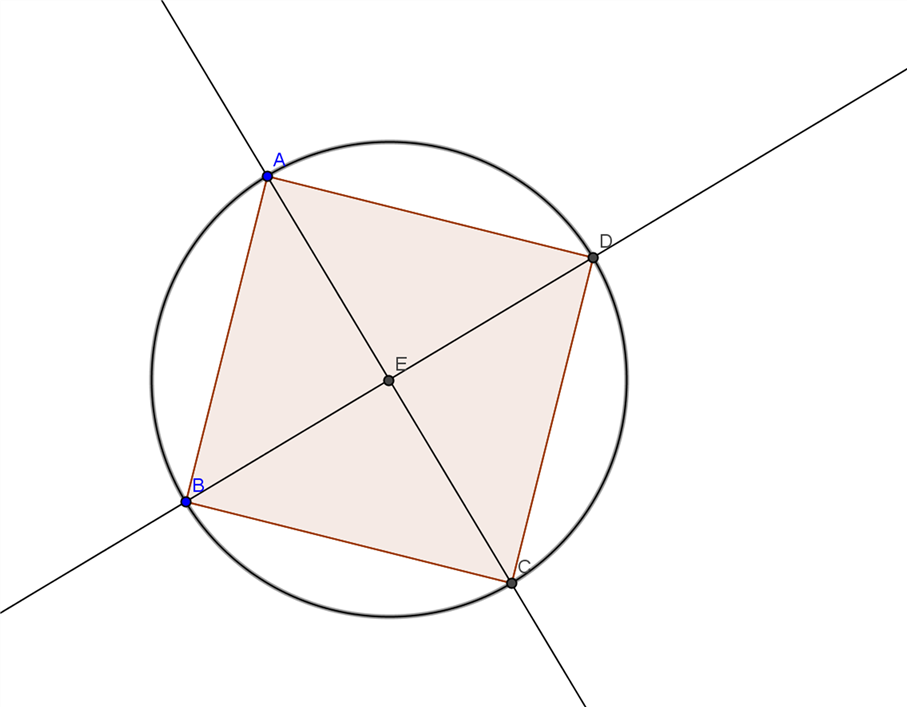
d) Kreis durch vier Punkte

Drei Punkte legen einen Kreis fest. Der vierte Punkt muss dann auch auf der Kreislinie liegen.

Aus vier beliebigen Punkten ist normalerweise kein Kreis konstruierbar. Ausnahme: Eckpunkte von Quadrat oder Rechteck.

 

Auftrag 3

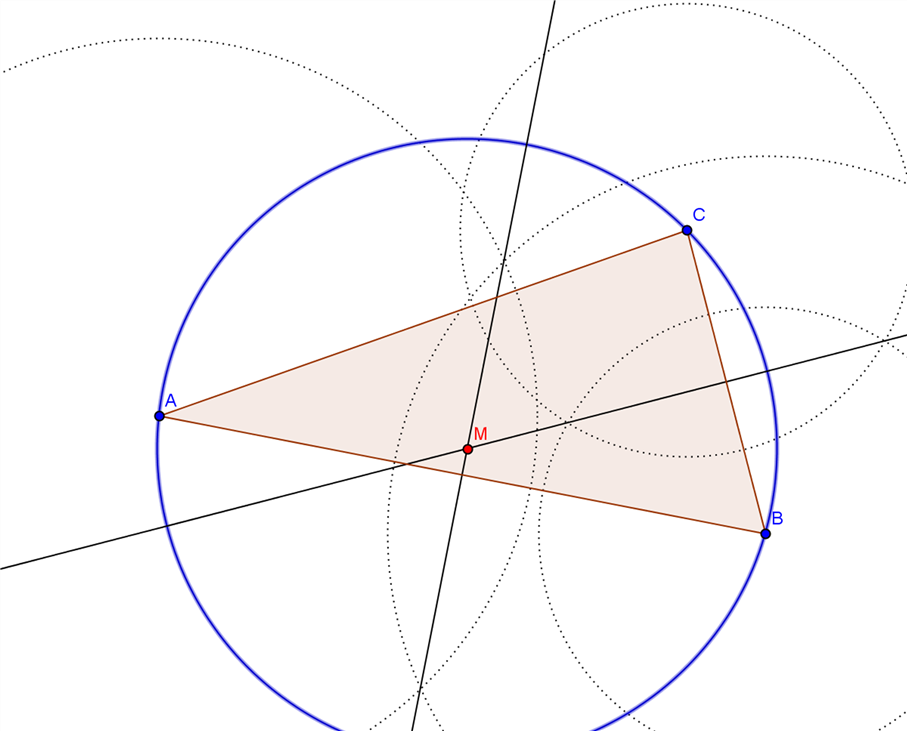
a) Dreieck ABC, Konstruktion des Punktes, der von allen Eckpunkten gleich weit entfernt ist: Umkreismittelpunkt

Konstruiere zwei Mittelsenkrechte, der Schnittpunkt ist der Umkreismittelpunkt.

 

b) Konstruktion eines Punktes, der von allen Eckpunkten in einem Viereck gleich weit entfernt ist geht nur, wenn a+b = g+d = 180°. Das Viereck heißt dann Sehnenviereck.

Auftrag 4

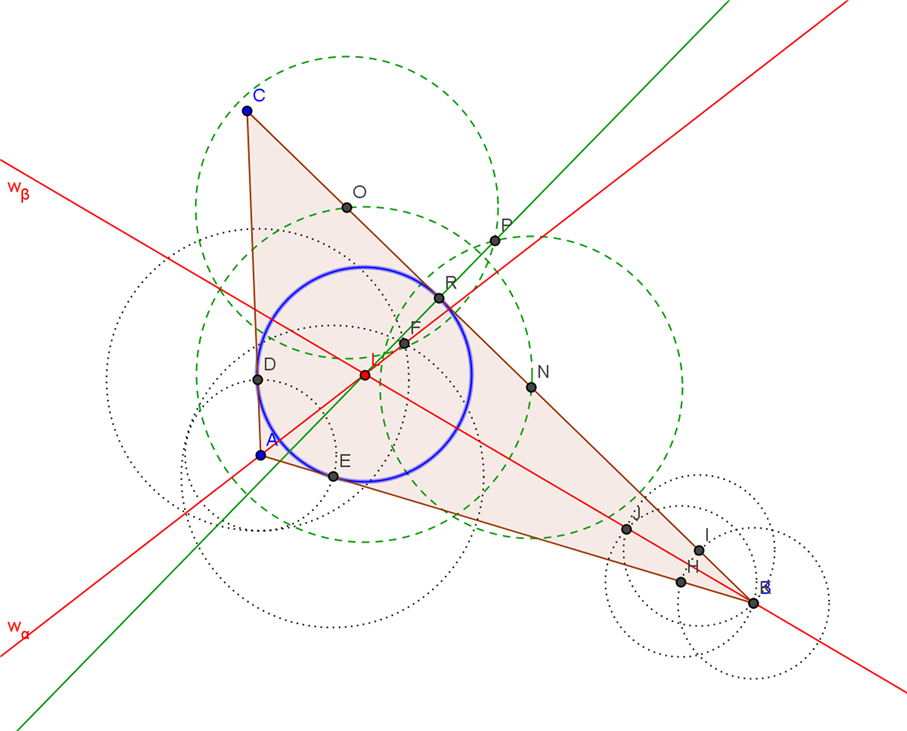
Inkreis

1. Konstruiere zwei Winkelhalbierende im Dreieck, der Schnittpunkt ist der Inkreismittelpunkt.
2. Um den Radius des Kreises zu erhalten, konstruiere vom Inkreismittelpunkt die Orthogonale auf eine der Dreiecksseiten (grüne Konstruktionslinien).

 

Auftrag 5

Der Schwerpunkt ist der Schnittpunkt der Seitenhalbierenden im Dreieck. Man kann beobachten, dass der Schwerpunkt die Seitenhalbierenden im Verhältnis 2 : 1 teilt.

(Zeichnung siehe Aufgabenblatt.)

Auftrag 6

Untersucht werden soll folgende Behauptung:

Die Winkelhalbierende w_a schneidet die Mittelsenkrechte m_a stets außerhalb des Dreiecks.

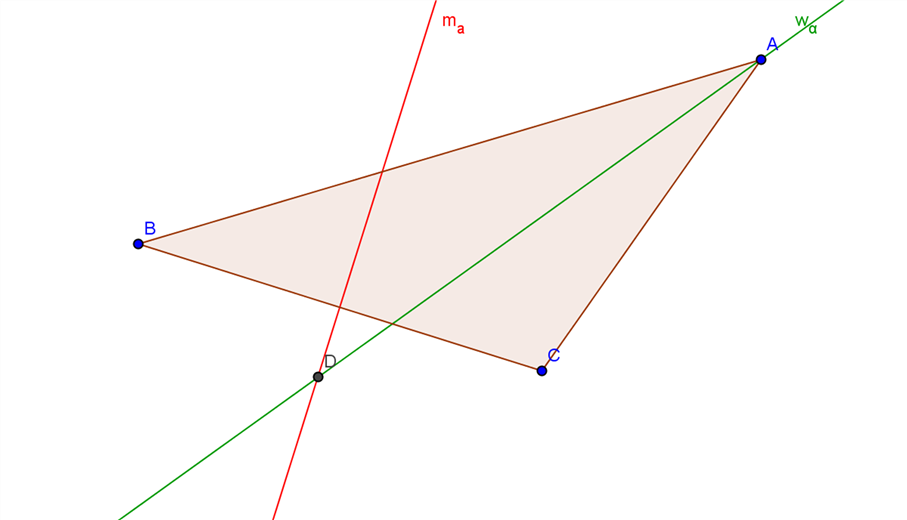
Man findet kein Dreieck, bei dem sich die beiden Geraden im Dreieck schneiden. Mit Ausnahme eines gleichschenkligen Dreiecks, wenn b und g gleich groß sind. Dann liegen Mittelsenkrechte und Winkelhalbierende aufeinander und es gibt unendlich viele Schnittpunkte, also auch im Dreieck.

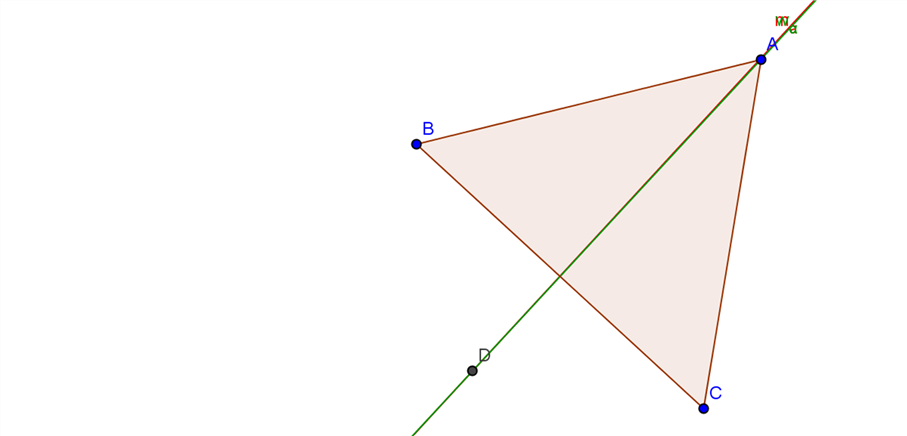
Auftrag 7

Gesucht ist ein Dreieck, bei dem Umkreismittelpunkt und Inkreismittelpunkt zusammenfallen.

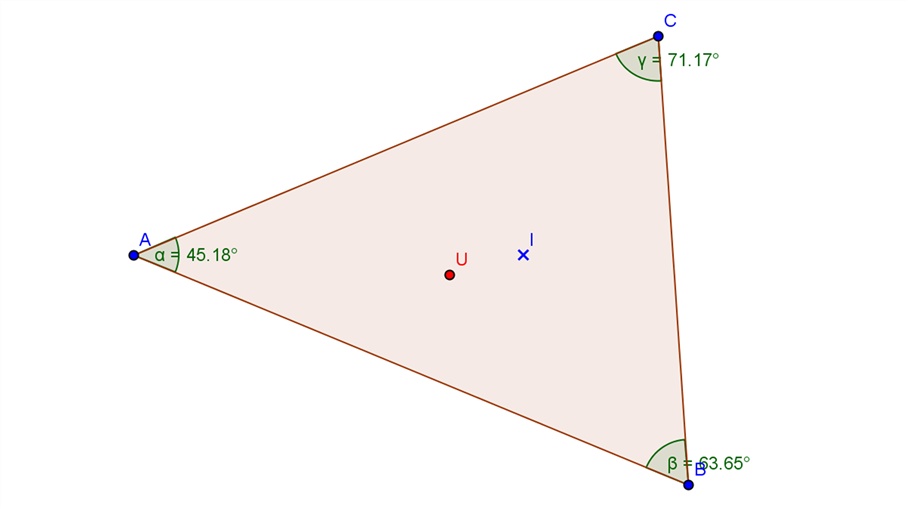
Die beiden Punkte fallen im gleichseitigen Dreieck zusammen:

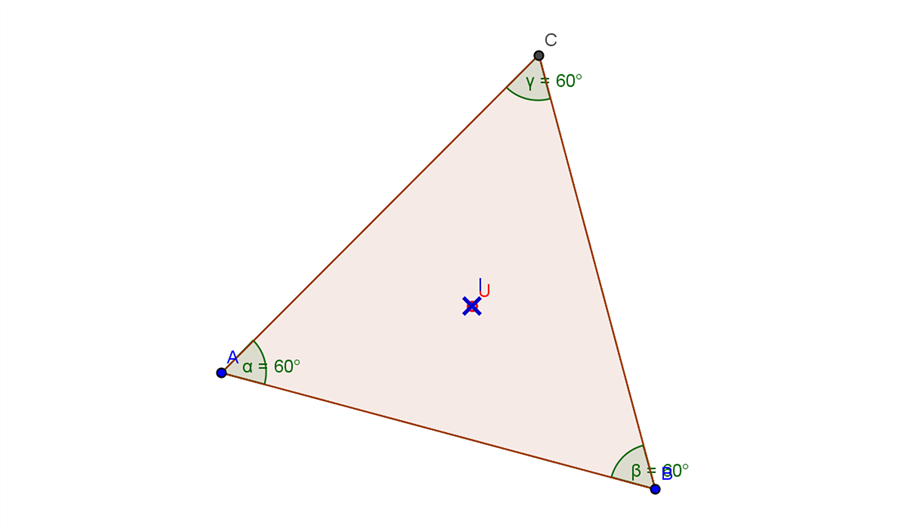
Auftrag 8

H: Höhenschnittpunkt

I: Inkreismittelpunkt (Schnittpunkt der Winkelhalbierenden)

S: Schwerpunkt (Schnittpunkt der Seitenhalbierenden)

U: Umkreismittelpunkt (Schnittpunkt der Mittelsenkrechten)

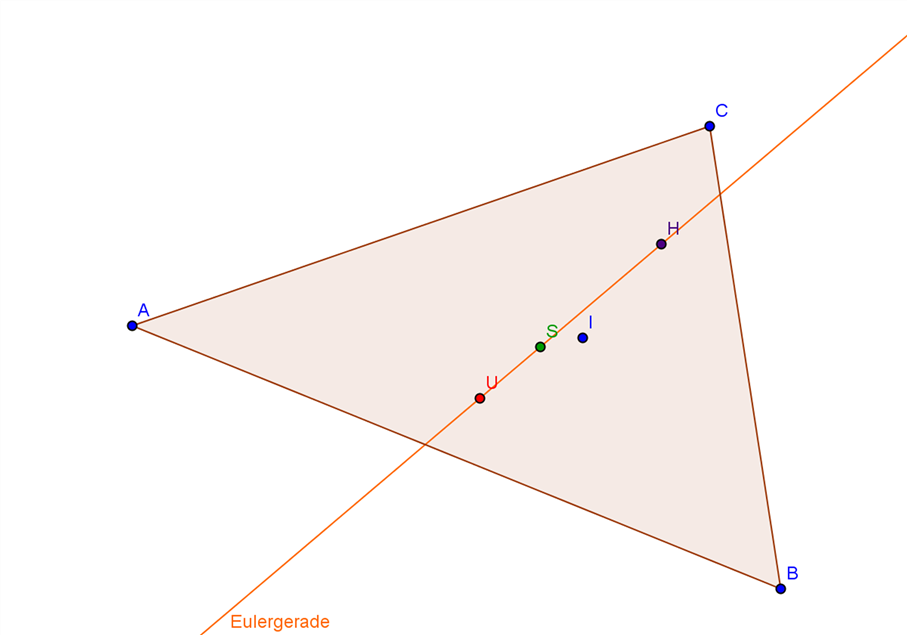
Hier lassen sich noch einmal alle bisherigen Beobachtungen machen, wie z.B. die besondere Lage der Punkte in speziellen Dreiecken (gleichseitig, gleichschenklig und rechtwinklig), außerdem stellt man fest, dass die Punkte U, S und H auf einer Gerade liegen, der sogenannten Euler-Gerade.

Wenn man auch Längen misst, sieht man, dass der Schwerpunkt auch die Strecke HU im Verhältnis 2 : 1 teilt.

Außerdem geht die Euler-Gerade auch durch den Mittelpunkt des Feuerbachkreises aus Aufgabe 9.

Auftrag 9

Feuerbachkreis

a) Konstruktion des Feuerbachkreises (Kreis durch die Seitenmitten)

b) Konstruktion des Mittelpunktes

1. Konstruiere den Höhenschnittpunkt (Orthogonale durch C zu Gerade AB, Orthogonale durch A zu Gerade BC)
2. Konstruiere die Seitenmitten (über Mittelsenkrechte – Schnittpunkt mit Seiten)
3. Konstruiere zu je zwei Seitenmitten die Mittelsenkrechte, der Schnittpunkt ist der Mittelpunkt des gesuchten Kreises.

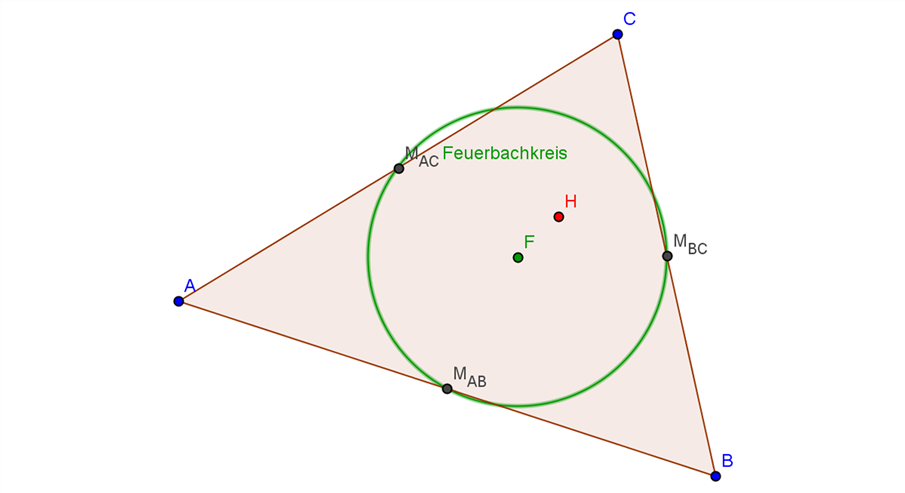
c) Der Feuerbachkreis geht genau dann durch eine Ecke des Dreiecks, wenn es an dieser Ecke einen rechten Winkel hat. Der Höhenschnittpunkt fällt dann mit dieser Ecke zusammen.

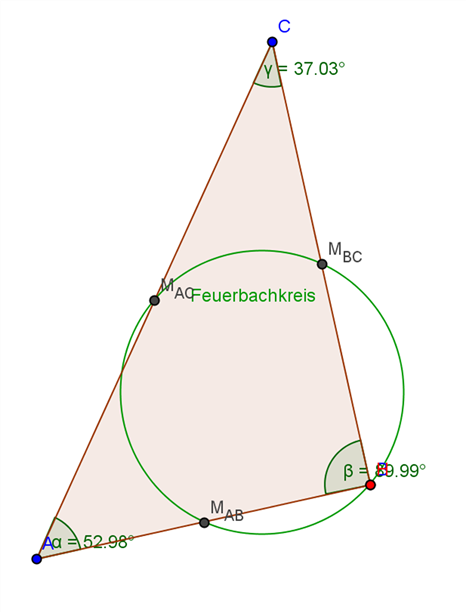
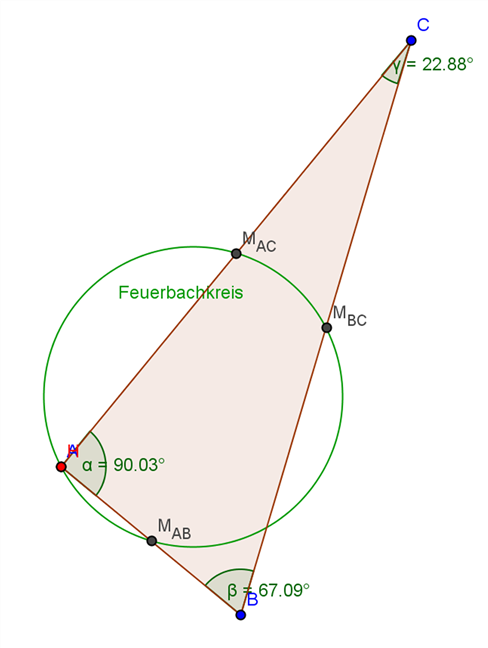
d) Der Feuerbachkreis berührt genau dann eine Dreiecksseite, wenn das Dreieck gleichschenklig ist. Der Kreis berührt die Basis des Dreiecks.

 

 

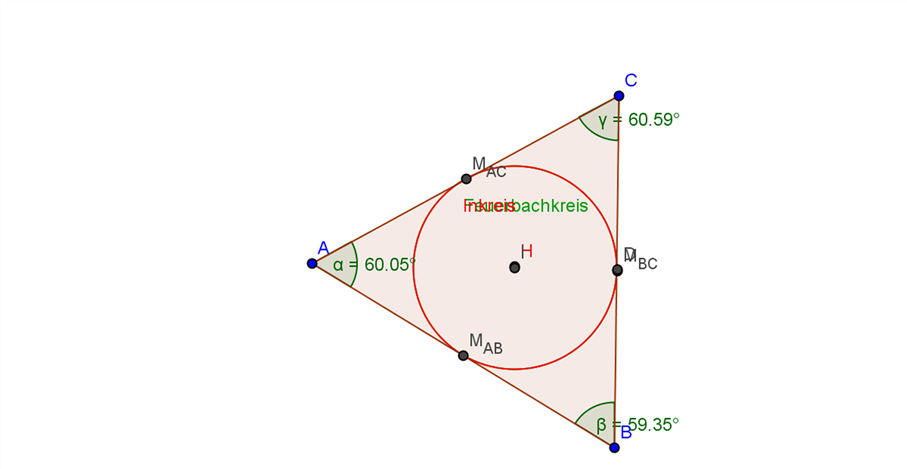
e) Der Inkreis stimmt mit dem Feuerbachkreis überein, wenn das Dreieck gleichseitig ist. Dann berührt der Feuerbachkreis genau wie der Inkreis die Dreiecksseiten in den Seitenmitten.

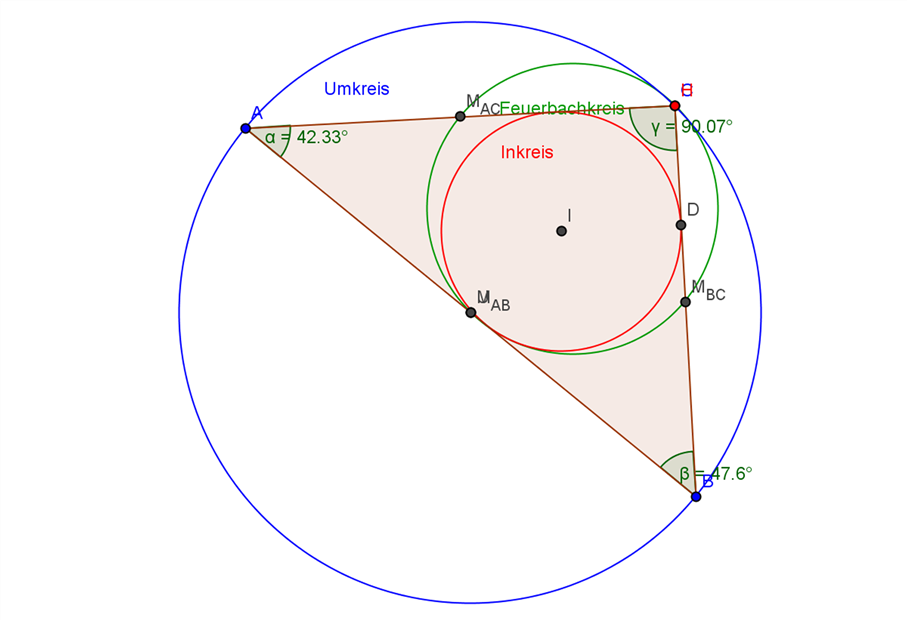
f) Im rechtwinkligen Dreieck berühren sich die beiden Kreise.

Der Mittelpunkt des Feuerbachkreises liegt auch auf der Euler-Geraden aus der letzten Aufgabe. Der Mittelpunkt F liegt genau in der Mitte zwischen U und H.

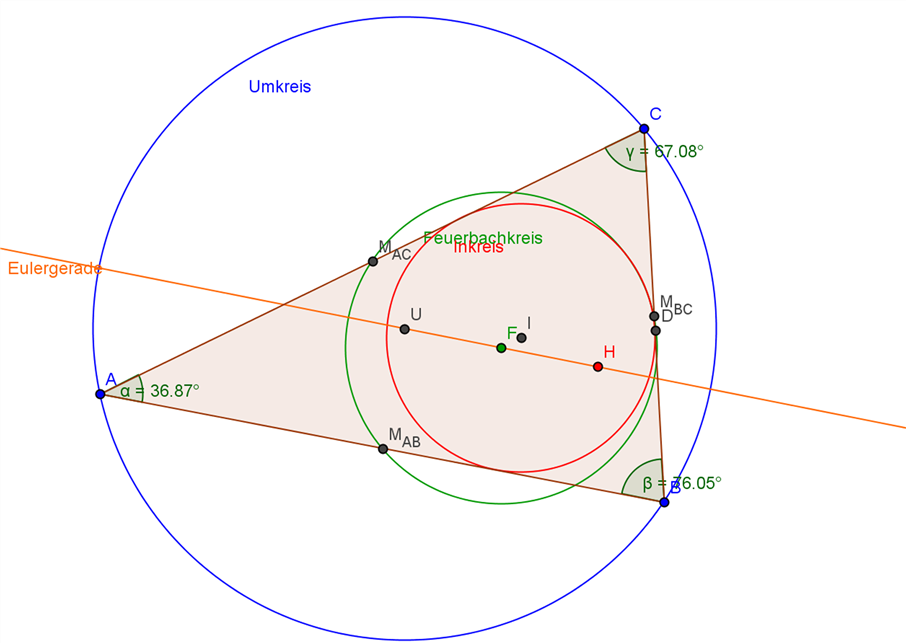
Wenn man die Radien der beiden Kreise (Feuerbachkreis und Umkreis vergleicht), so sieht man, dass der Radius des Umkreises immer genau doppelt so groß ist, wie der des Feuerbachkreises.

 

Musterlösung: Herunterladen [pdf][1 MB]

 

Weiter zu Informationen zur Fortbildung