Beispiele zur Kombinatorik
In einer Schale befinden sich sechs (n) verschieden farbige Spielsteine.
Piller, März 2018
1. Ziehen mit Zurücklegen – mit Beachtung der Reihenfolge
Piller, März 2018
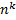
Es wird dreimal (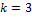
) mit Zurücklegen aus den sechs (
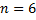) Spielsteinen gezogen.
Die Farbreihenfolge wird berücksichtigt.
Bestimme wie viele verschiedene Kombinationsmöglichkeiten es gibt.
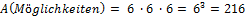
Weiteres Beispiel: Zahlenschloss
2. Ziehen ohne Zurücklegen – mit Permutation
Piller, März 2018
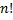
Es wird sechsmal (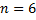) ohne Zurücklegen gezogen.
Die sechs Steine werden mit Beachtung der Farbreihenfolge aneinandergelegt.
Bestimme wie viele mögliche Anordnungen es gibt.
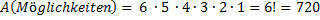
Weiteres Beispiel: Laufbahnproblematik
3. Ziehen ohne Zurücklegen – mit Beachtung der Reihenfolge
Piller, März 2018
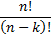
Es wird dreimal (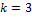) ohne Zurücklegen aus den sechs Steinen
(
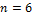) mit Beachtung der Farbreihenfolge gezogen.
Bestimme wie viele mögliche Anordnungen es für die drei aus sechs Steinen gibt.
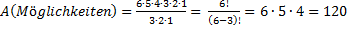
Weiteres Beispiel: Platzierungsproblematik
4. Ziehen mit einem Griff - ohne Beachtung der Reihenfolge
Piller, März 2018
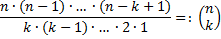
Es werden vier (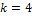
) aus den sechs (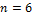) Spielsteinen auf einmal gezogen.
Die Reihenfolge der Farben spielt keine Rolle.
Bestimme wie viele mögliche Anordnungen drei aus sechs es gibt.
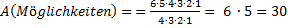
Weiteres Beispiel: Lottoproblem
Da bei allen angegebenen Formeln alle Kombinationen mit gleicher Häufigkeit auftreten, können mit Laplace die entsprechenden Wahrscheinlichkeiten bestimmt werden.
Insbesondere gilt das für das sogenannte „Lottoproblem“:
Wenn aus einer Gruppe von 16 Mädchen und 12 Jungen eine Sechsergruppe zufällig gebildet wird, ist die Wahrscheinlichkeit dafür, dass 4 Mädchen und 2 Jungen ausgewählt werden:
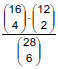
Das Lottoproblem lässt sich nicht mehr im Wortlaut der inhaltsbezogenen Kompetenzen durch „einfache kombinatorische Überlegungen“ lösen. Es lässt sich vielmehr mithilfe einer Kombination „einfacher kombinatorischer Überlegungen“ lösen.
In diesem Sinne ist das Lottoproblem durch „Verarbeiten komplexer Sachverhalte“ unter Berücksichtigung der prozessbezogenen Kompetenzen „Modellieren“ und „Problemlösen“ in Klasse 10 im Anforderungsbereich III anzusiedeln.
Das Lottoproblem muss im Unterricht der Klasse 10 nicht thematisiert werden, da es die im Bildungsplan angewiesenen inhaltsbezogenen Kompetenzen nicht explizit abdeckt.
Unabhängig davon könnte - bei nicht im Unterricht thematisiertem Lottoproblem - eine solche Fragestellung in einer Klassenarbeit im Sinne der Transferleistung im Anforderungsbereich III bzw. einer kompetenzorientierten Klassenarbeit auftauchen.
Kombinatorik: Herunterladen [pdf][415 KB]
Weiter zu Geometrie