Lö­sun­gen

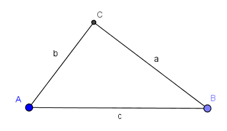
a) a = 4 cm; b = 3 cm; c = 5 cm

a² + b² = 4² + 3²  = 25

c² = 5² = 25

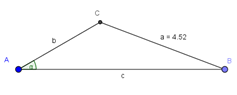
b) b = 3,2 cm; c = 7 cm; α = 30°

a² + b² = 4,5² + 3,2²  = 30,49

c² = 7² = 49

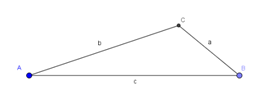
c) a = 3 cm; b = 6 cm; c = 8 cm

a² + b² = 3² + 6² = 45

c² = 8² = 64

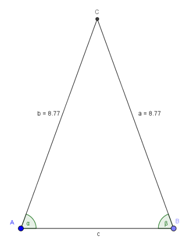
d) c = 6 cm; α = β = 70°

 a² + b² = 8,8² + 8,8² =  154,88

 c² = 6² = 36

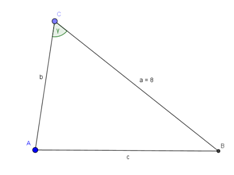
e) a = 2,5 cm; b = 6 cm; γ = 90°

a² + b² = 2,5² + 6² = 42,25

c² = 6,5² = 42,25

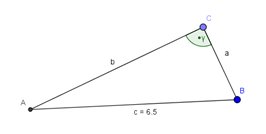
f) b = 5 cm; c = 7 cm; γ = 60°

a² + b² = 8² + 5² = 89

c² = 7² = 49

a) a = 4 cm; b = 3 cm; c = 5 cm

 Kon­struk­ti­ons­schrit­te:

1. Zeich­ne die Stre­cke c mit c = 5 cm.

2. Zeich­ne einen Kreis um A mit r = b = 3 cm.

3. Zeich­ne einen Kreis um B mit r = a = 4 cm.

4. Der Schnitt­punkt der bei­den Krei­se ist C.

b) b = 3,2 cm; c = 7 cm; α = 30°

 Kon­struk­ti­ons­schrit­te:

1. Zeich­ne die Stre­cke c mit c = 7 cm.

2. Trage in A den Win­kel α mit α = 30° ab.

3. Trage auf dem frei­en Schen­kel von α die Stre­cke b mit b = 3,2 cm ab.

4. Der End­punkt der Stre­cke ist C.

c) a = 3 cm; b = 6 cm; c = 8 cm

 Kon­struk­ti­ons­schrit­te:

1. Zeich­ne die Stre­cke c mit c = 8 cm.

2. Zeich­ne einen Kreis um A mit r = b = 6 cm.

3. Zeich­ne einen Kreis um B mit r = a = 3 cm.

4. Der Schnitt­punkt der bei­den Krei­se ist C.

d) c = 6 cm; α = β = 70°

 Kon­struk­ti­ons­schrit­te:

1. Zeich­ne die Stre­cke c mit c = 6 cm.

2. Trage in A den Win­kel α mit α = 70° ab.

3. Trage in B den Win­kel β mit β = 70° ab.

4. Der Schnitt­punkt der bei­den frei­en Schen­kel ist C.

e) a = 2,5 cm; b = 6 cm; γ = 90°

 Kon­struk­ti­ons­schrit­te:

1. Zeich­ne die Stre­cke b mit b = 6 cm.

2. Trage in C den Win­kel γ mit γ = 90° ab.

3. Trage auf dem frei­en Schen­kel von γ die Stre­cke a mit a = 2,5 cm ab.

4. Der End­punkt der Stre­cke ist B.

f) b = 5 cm; c = 7 cm; γ = 60°

 Kon­struk­ti­ons­schrit­te:

1. Zeich­ne die Stre­cke b mit b = 5 cm.

2. Trage in C den Win­kel γ mit γ = 60° ab.

3. Zeich­ne einen Kreis um A mit r = c = 7 cm.

4. Der Schnitt­punkt des Krei­ses mit dem frei­en Schen­kel ist B.