LGS im Basisfach
Im Gegensatz zum bisherigen vierstündigen Kernfach wird im Basisfach die Berechnung der Lösung eines linearen Gleichungssystems nur im Falle dessen eindeutiger Lösbarkeit verlangt. Das Gaußverfahren wird daher in allen anderen Fällen nur bis zur Stufenform angewandt, um dann auf dieser Grundlage eine Aussage zu machen, ob das lineare Gleichungssystem keine oder unendlich viele Lösungen besitzt. Eine Beschränkung auf lineare 3x3 Gleichungssysteme kann bei der prinzipiellen Betrachtung des Lösungsverfahrens sinnvoll sein. Bei der Bestimmung von ganzrationalen Funktionen zu vorgegebenen Eigenschaften sollten Fälle betrachtet werden, bei denen sich die Zahl der Unbekannten rasch reduziert.
Die Notation einer Lösungsmenge wird in keinem der Fälle erwartet. Ebenso wird daher auch nicht erwartet, dass die Schülerinnen und Schüler eine solche Lösungsmenge geometrisch interpretieren können. Eine geometrische Überlegung kann jedoch zur Unterscheidung der Fälle „keine Lösung“ und „unendlich viele Lösungen“ sinnvoll sein (siehe unten).
Die folgenden Aufgabentypen sind demnach denkbar. Sie sind aber selbstverständlich nicht als abschließende Liste zu verstehen, sondern wollen vielmehr Optionen aufzeigen.
Aufgabe 1:

Lösung: Man formt das LGS grundsätzlich mit dem Gauß-Algorithmus um bis zur Stufenform:
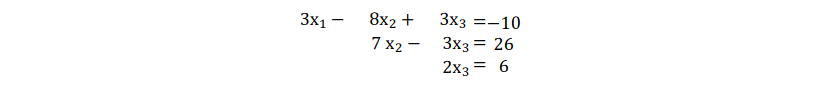
Und setzt in diesem Fall nach oben ein und erhält: x1= 7,x2= 5und x3= 3.
Aufgabe 2:

Lösung: Der Gauß-Algorithmus bis zur Stufenform führt auf folgendes lineare Gleichungssystem:
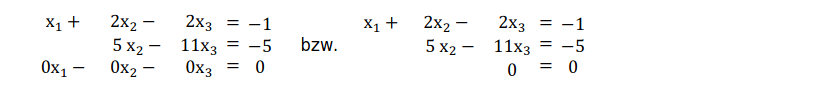
Die letzte Zeile ist hier eine „Nullzeile“ und in keiner der beiden anderen Zeilen steht eine falsche Aussage, wie z.B. 0x1+0x2+ 0x3= −5 , daher hat das lineare Gleichungssystem unendlich viele Lösungen. Insbesondere hat also das obige lineare Gleichungssystem keine eindeutige Lösung.
Im Unterricht kann zur Begründungdieses Sachverhalts ein formales Einsetzen verschiedener Werte oder eine geometrische Interpretation verwendet werden, wobei beachtet werden muss, dass letztere im Bildungsplan nicht als Kompetenz gefordert wird. Geometrisch könnteman dann die beiden verbleibenden Gleichungen als Ebenengleichungen interpretieren. Diese beiden Ebenen sind nicht parallel und schneiden sich daher in einer Gerade, woraus folgt, dass das das lineare Gleichungssystemunendlich viele Lösungenhat.
Aufgabe 3:

Lösung: Man formt das LGS wieder mit dem Gauß-Algorithmus um bis zur Stufenform:
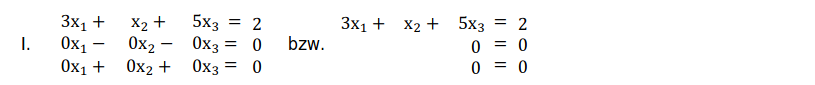
Der Gaußalgorithmus führt auf ein lineares Gleichungssystemmit zwei Nullzeilen, d.h. es gibt unendlich viele Lösungen.
Begründung: Geometrisch kann man die 3 Zeilen des gegebenen linearen Gleichungssys-tems als Ebenengleichungen von 3 identischen Ebenen interpretieren. Das lineare Glei-chungssystem hat damit unendlich viele Lösungen.
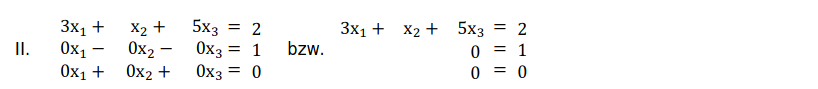
Die letzteZeile ist hier eine „Nullzeile“ und in der 2. Zeile steht die falsche Aussage 0x1+0x2+ 0x3= 1 , daher hat das lineare Gleichungssystem keine Lösung.
Begründung: Geometrisch kann man die 3 Zeilen des gegebenen linearen Gleichungssystems als Ebenengleichungen von 2 identischen Ebenen und einer dazu parallelen Ebene interpretieren. Daher haben die 3 Ebenen keine gemeinsamen Punkte und das lineare Gleichungssystem hat damit keine Lösung.
Aufgabe 4:

Lösung: Man formt das LGS wieder mit dem Gauß-Algorithmus um bis zur Stufenform:
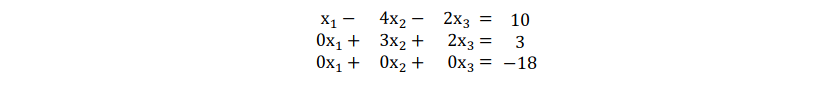
Der Gaußalgorithmus führt auf ein lineares Gleichungssystem, das in der letzten Zeile die falsche Aussage 0=−18 enthält. Deshalb ist das lineare Gleichungssystem unlösbar.
Im Unterricht bietet sich hier zur Begründung keine geometrische Interpretation in Bezug auf die Lage der drei gegebenen Ebenen an.
Selbstverständlich sind die in diesem Abschnitt genannten Fragestellungen alle auch im Leistungsfach möglich.
Ergänzende Hinweise: Herunterladen [pdf][487 KB]
Weiter zu LGS im Leistungsfach
