Namensgeheimnis der Kegelschnitte
In der sechsten Stunde der Einheit werden die nicht zerfallenden Kegelschnitte Ellipse, Parabel und Hyperbel mit einem DGS gezeichnet und deren Namensgeheimnis aufgedeckt. Als mögliche Vertiefung zur Verzahnung der geometrischen und algebraischen Welt kann in Aufgabe 4 auch eine allgemeine Kegelschnittsgleichung in (Scheitellage) hergeleitet werden.
In Aufgabe 1 werden alle drei Kegelschnittsarten im Rahmen einer Kegelschnitt-Schar gezeichnet, um die besondere Eigenschaft der Parabel als Grenzlinie zwischen Ellipsen und Hyperbeln zu betonen. Im a)-Teil wird die in Brennpunktlage vorgegebene Schargleichung begründet, bevor diese dann im b)-Teil von den SuS verwendet wird, um einzelne Kurven der Schar mithilfe von GeoGebra zeichnen zu lassen:
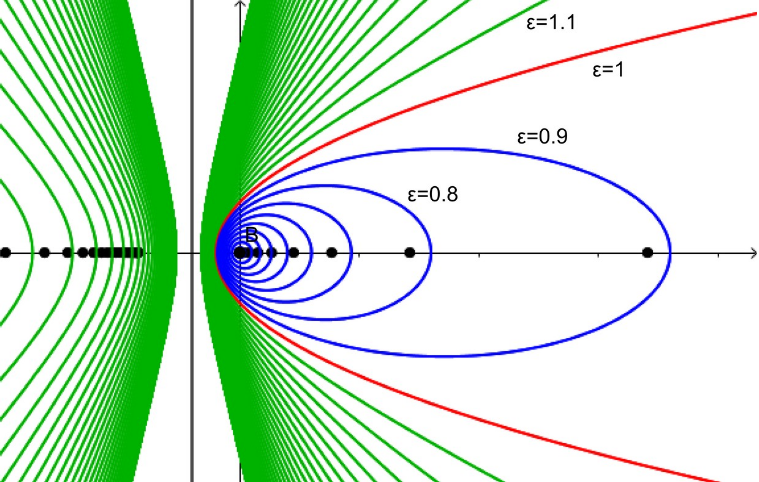
Zur Unterscheidung der Kegelschnittsarten wurde die bereits bekannte numerische Exzentrizität ε als Scharparameter gewählt. Im Rahmen eines Zusatzauftrags können die SuS auch das Prinzip der dynamischen Farbgebung erkunden. Die verwendete Färbung entspricht dabei der durchgehenden Farbcodierung innerhalb der Einheit: Ellipsen werden blau, Hyperbeln grün und die Parabel als Grenzlinie rot gefärbt.
Aufgabenteil c) kann als differenzierender Zusatzauftrag zur anschließenden Reflexion genutzt werden. Im Unterrichtsgespräch könnte man auch die im Erwartungshorizont beschriebene Wanderung des zweiten Brennpunktes thematisieren, der bei der Parabel als Fernpunkt im Unendlichen liegt. Dies ließe sich zur Vertiefung auch mit Definitionslücken (Polstellen) in Verbindung bringen, bei denen ebenfalls ein Durchgang durchs Unendliche mit Vorzeichenwechsel erfolgen kann.
Aufgabe 2 geht über das Kerncurriculum hinaus. Die Namen Ellipse, Parabel und Hyperbel wurden von den altgriechischen Verben für „ermangeln“, „gleichkommen“ und „übersteigen“ abgeleitet. Diese Aufgabe bietet den SuS die Gelegenheit, dieses "Namensgeheimnis" zu lüften. Frau Haftendorn spricht hier zugespitzt von einem Geheimnis, da man auch heute noch einigen falschen Deutungen begegnet wie z.B. der Auffassung, dass es der Ellipse an Kreisform mangele oder dass bei der Hyperbel die Schnittebene "übermäßig" steil verliefe (vgl. [HAFT2], Kap 7.4., S. 197). Tatsächlich lässt sich der Namensursprung durch den Flächenvergleich des Ordinatenquadrats mit Flächeninhalt y2 und des Sperrungsrechtecks mit Flächeninhalt 2px sehr anschaulich motivieren, wie ein kurzer Blick in den Erwartungshorizont zeigt:
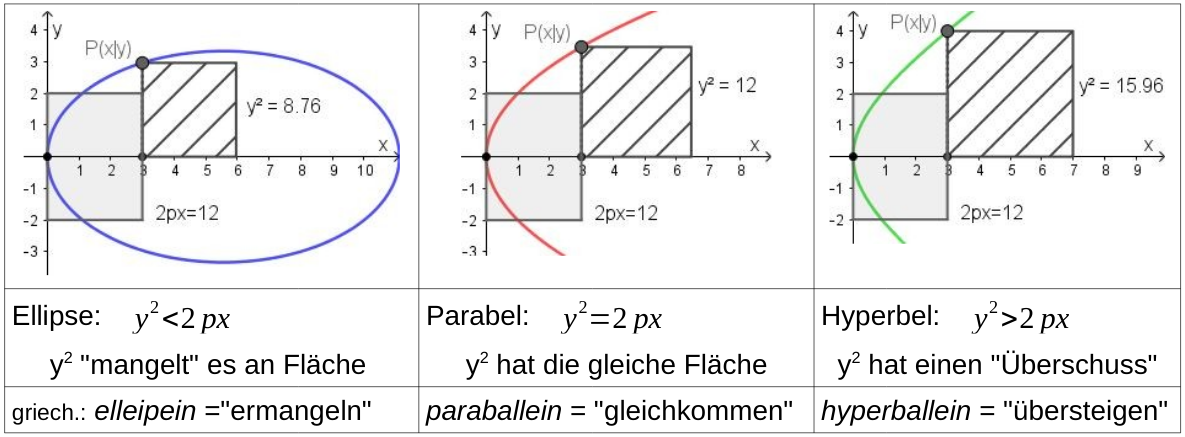
An dieser Stelle lohnt sich der fächerübergreifende Bezug zur Sprachwissenschaft: Das Stilmittel der Einsparung von Satzteilen wie z.B. "Läuft" statt "Es läuft gut" wird allgemein als Ellipse bezeichnet. Unter einer Hyperbel versteht man dagegen eine Übertreibung wie "himmelhoch" oder "wie Sand am Meer". Und in der Literatur begegnet man Parabeln in Form von gleichnishaften belehrenden Erzählungen, wie wir sie von zahlreichen Autoren kennen.
Für die unterrichtliche Umsetzung steht das Applet M10geo_Nr2_Namensgeheimnis.ggb1 zur Verfügung, mit dem die SuS sich im stärker gelenkten a)-Teil zunächst die geometrische Interpretation der Parabelgleichung erschließen können, während im etwas offener gehaltenen b)-Teil dann das Ordinatenquadrat und Sperrungsrechteck für verschiedene Ellipsen und Hyperbeln verglichen werden, um so den jeweiligen Mangel bzw. Überschuss an Fläche zu entdecken. Nach einer Präsentation durch einzelne SuS kann die Ergebnissicherung mit der vorbereiteten Tabelle auf der folgenden Seite der Materialdatei erfolgen.
Aufgabe 3 bietet optional noch die Möglichkeit, in GeoGebra die Hüllkurve einer Parabel nach Anleitung zu konstruieren und dabei die geometrischen Zusammenhänge zu vertiefen. Die Aufgabe kann als Hausaufgabe oder im Unterricht differenzierend eingesetzt werden. Auch die einzelnen Teilaufgaben lassen sich dabei beliebig erweitern oder eingrenzen. So könnte beispielsweise die im d)-Teil eingebundene Animationsvariante entweder vertieft oder ganz gestrichen werden.
Mögliche Vertiefung: Allgemeine Scheitelgleichung der Kegelschnitte
Mit Aufgabe 4 kann die Herleitung einer allgemeinen Scheitelgleichung der Kegelschnitte realisiert werden, um die algebraischen Kompetenzen der SuS zu fördern. Hierzu wurde wieder eine lückenhafte Umformungskette in Zweispaltenform eingebunden, die bei Bedarf noch auf die eigene Lerngruppe abgestimmt werden kann. Falls man eine interessierte und leistungsstarke Gruppe vor sich hat, in der die SuS in Hinblick auf die Wahl des fünfstündigen Leistungsfaches gerne ihre algebraischen Kompetenzen ausbauen möchten, besteht hier die Gelegenheit, Parameter als "Formvariablen" in ihrer ursprünglichen Bedeutung zu erleben, als Variablen, die die Form eines Kegelschnitts bestimmen. Dabei können diverse Parametertransformationen gedeutet und so beispielsweise die Zusammenhänge zwischen Halbparameter p und numerischer Exzentrizität ε vertieft werden. Im Umgang mit den Kegelschnitten könnten so wertvolle Vorstellungen zu Scharkurven verankert werden, was bei später folgenden klassischen Kurvendiskussionen nicht so ohne Weiteres der Fall sein dürfte.
Unterrichtsverlauf: Herunterladen [odt][4.8 MB]
Unterrichtsverlauf: Herunterladen [pdf][2.3 MB]
1Die Datei findet man im Materialpaket unter M03_geo/3_vorlagen_tauschordner oder kann sie direkt im GeoGebra-Buch IMP10 unter https://www.geogebra.org/m/qqfbwvmr aufrufen.
Weiter zu Ellipsen und Hyperbeln
