Ellipsen und Hyperbeln

In der siebten Stunde soll die Mittelpunktsgleichung einer Ellipse anschaulich hergeleitet und daraus die Gleichung einer Hyperbel abgeleitet werden. Um dieses Minimalziel zu erreichen, ist die Bearbeitung der Aufgaben 1 und 3 vorgesehen. Im Material sind zusätzlich Ergänzungen und Vertiefungsangebote eingearbeitet, die Anknüpfungspunkte in mehrere Richtungen bieten.

Aufgabe 1 nutzt erneut das didaktische Konzept der Rasterlinien, um diskrete Punkte von Ellipsen und Hyperbeln zu zeichnen und ermöglicht so einen anschaulichen Einstieg. Dabei wird ein einzelner Rasterpunkt P vorgegeben und dessen Abstandsumme (bzw. - differenz) zu den Brennpunkten bestimmt. Durch das Einzeichnen von Rasterpunkten gleicher Abstandssumme (bzw. -differenz) nehmen Ellipse bzw. Hyperbel Punkt für Punkt Gestalt an. Die SuS entdecken dabei ohne formalen Nachweis die Brennpunktsdefinition von Ellipse und Hyperbel. Der b)- und c)-Teil halten differenzierende Zusatzaufträge bereit, die auch nur von einzelnen SuS bearbeitet werden können. Dabei sollte allerdings das Ergebnis des c)-Teils besprochen und schon hier gesichert werden: Die Abstandssumme einer Ellipse (bzw. -differenz einer Hyperbel) entspricht immer dem Abstand 2a der beiden Hauptscheitel.

Mögliche Vertiefung: Beweis der Konstanz der Abstandsumme (bzw. -differenz)

Der Beweis mithilfe der Dandelinschen Kugeln ginge über das Kerncurriculum hinaus. Als motivierendes Beispiel für eine sehr elegante Argumentation sollte er interessierten SuS im Sinne der Differenzierung aber nicht vorenthalten werden. Der Beweisgang wurde beim fachlichen Hintergrund in Abschnitt 2.5 bereits dargestellt. Er eignet sich auch als differenzierender Zusatzauftrag oder GFS-Thema für interessierte SuS. Für die Umsetzung steht das Applet M10geo07_Beweis_Dandelin.ggb¹ zur Verfügung, mit dem sich die Kernidee dynamisch visualisieren lässt:

Man kann die für die Argumentation erforderlichen Strecken ein- und ausblenden und den Punkt P auf dem jeweiligen Kegelschnitt (Ellipse oder Hyperbel) wandern lassen.

Die Ansicht kann "auf Knopfdruck" (Ändern der Blickrichtung in der Gestaltungsleiste der 3D-Ansicht) so ausgerichtet werden, dass die orthogonale Projektion auf eine der drei Koordinatenebenen zu sehen ist (vgl. Bild rechts). Der gezielte Wechsel zwischen Querschnitt und Schrägbild ermöglicht es, die Argumentation visuell optimal zu unterstützen. Die Lage der beiden Brennpunkte als Berührpunkte der Dandelinschen Kugeln sollte den SuS beispielsweise auch im Querschnitt gezeigt werden, um die räumliche Interpretation zu erleichtern.

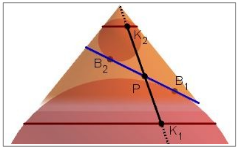
Analog ließe sich mit dem Applet auch die konstante Abstandsdifferenz der Hyperbel dynamisch visualisieren und begründen, was aber nicht für den Unterricht im Plenum empfohlen wird. Da die Argumentation zur Abstandsdifferenz für die SuS schwieriger zu erfassen ist, sollte diese Vertiefung eher einzelnen, sehr motivierten SuS vorbehalten bleiben.

Aufgabe 2 eröffnet alternativ oder ergänzend die Möglichkeit, einen enaktiven Zugang über die Fadenkonstruktionen von Ellipse und Hyperbel zu wählen. Aus didaktischer Sicht könnte man nach der Konstruktion diskreter Punkte im a)-Teil nun mithilfe der Fadenkonstruktionen Ellipsen und Hyperbeln als stetige Kurven konstruieren, deren algebraische Beschreibung dann in Aufgabe 3 folgt. Die klassische Gärtner-Konstruktion liefert dank ihrer robusten und einfachen Umsetzung schnell qualitativ sehr gute Ergebnisse und sollte auf jeden Fall irgendwo in der Einheit ihren Platz finden. Wenn man Zeit hat, lohnt sich der relativ überschaubare Aufwand der Herstellung aber auch für einen Hyperbelzirkel². Dazu bräuchte man dann zwar etwas mehr Unterrichtszeit, würde aber inhaltlich gleichzeitig die Leitkreis-Konstruktion von Ellipse und Hyperbel vorentlasten, die in der nachfolgenden Stunde im Computerraum erarbeitet werden könnte.

Die anschauliche Herleitung der Mittelpunktsgleichung der Ellipse in Aufgabe 3 fußt auf den vorhandenen intuitiven Vorstellungen zur orthogonalen Affinität. Die Ellipse kann als affines Bild eines Kreises aufgefasst werden. Der Einfachheit halber beschränkt man sich hier auf eine orthogonale Achsenaffinität, mit der die SuS bereits ausreichend Erfahrungen gesammelt haben, z.B. bei der Streckung bzw. Stauchungen von Parabeln in Klasse 9 oder ggf. auch Amplituden periodischer Funktionen in Klasse 10.

Im a)-Teil wird zunächst der Satz des Pythagoras aktiviert, um die Kreisgleichung zu motivieren und in Form der späteren Mittelpunktsgleichung zu begründen. Im b)-Teil ermitteln die SuS den zur Stauchung passenden Streckfaktor. Man sollte wie im Erwartungshorizont beschrieben die Stauchung von y‘ zu y (vom Kreis zur Ellipse) auch umgekehrt als Streckung von y zu y‘ (von der Ellipse zum Kreis) interpretieren, um die Herleitung im c)-Teil vorzuentlasten. Die Aufgabenstellung des c)-Teils enthält in der Fassung für alle IMP-Klassen klare Anweisungen und ist damit relativ eng formuliert. Dies soll der Tatsache Rechnung tragen, dass die SuS bisher noch wenig Erfahrung mit algebraischen Beschreibungen von Ortskurven haben. Man kann und sollte die Aufgabe angemessen öffnen, um sie auf die eigene Klasse abzustimmen.

Die Hyperbelgleichung könnte dann wie im d)-Teil gefordert in einer Tablet-Arbeitsphase oder auf Zuruf an einem Demonstrationsrechner durch Variation der Eingabe in einem DGS gewonnen werden, bevor abschließend beide Mittelpunktsgleichungen im Merksatz gesichert werden.

Mögliche Ergänzungen für alle SuS

Mit Aufgabe 4 kann man in einem einfachen Transfer den Flächeninhalt einer Ellipse erarbeiten lassen, um auch hier den Zusammenhang zum bekannten Kreisinhaltzu reflektieren, indem die SuS den Kreis nun als Spezialfall einer Ellipse erkennen. Sie sollten dafür auch die formale Bedingung kennen, dass beide Halbmesser gleich groß sind (a = b = r).

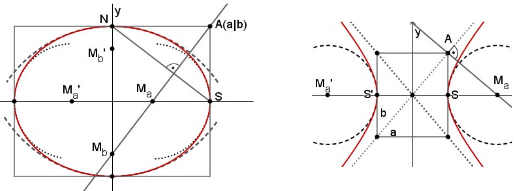
Aufgabe 5 hält einen praktischen und hoffentlich motivierenden Zugang bereit und ist für alle Klassen geeignet, die Spaß am Zeichnen haben. Nebenbei lernen die SuS weitere interessante Eigenschaften von Ellipsen und Hyperbeln kennen. Auch im Zeitalter der allgegenwärtigen Computernutzung ist die Frage nach analogen Lösungen nach wie vor wichtig. Hier geht es also um die händische Erstellung von ästhetisch ansprechenden sorgfältig gezeichneten Ellipsen und Hyperbeln. Dabei kommt man an den hilfreichen Scheitelkrümmungskreisen nicht vorbei. An zwei konkreten Beispielen wird erklärt, wie man deren Mittelpunkte und Radien bestimmt und sie anschließend verwendet, um Ellipsen und Hyperbeln möglichst genau anzunähern³.

Die Beschäftigung mit den Scheitelkrümmungskreisen liefert darüber hinaus einen ersten Zugang zu den interessanten um- und einbeschriebenen Rechtecken von Ellipsen und Hyperbeln, die in Aufgabe 5 vorgegebenen wurden. Aus einem Rechteck mit den Seitenlängen 2a und 2b kann immer die zugehörige Ellipse oder Hyperbel mit den Halbmessern a und b konstruiert werden. Die verlängerten Diagonalen des Rechtecks können dabei als Asymptoten der zugehörigen Hyperbeln entdeckt werden. In einem Exkurs könnte auch die bekannte Normalhyperbel y=1/x und durch den Spezialfall a=b charakterisiert werden⁴.

Die Aufgaben 8 und 9 bieten einen enaktiven Zugang zur Leitkreis-Konstruktion von Ellipsen und Hyperbeln über das Falten von Hüllkurven wie bei der Parabel⁵. Durch den Einsatz als Hausaufgabe könnte man die zeitintensive Faltarbeit wieder auslagern, so dass die daran anknüpfenden Leitkreis-Konstruktionen von Ellipse und Hyperbel in der optionalen Folgestunde einfacher und sinnbehafteter erarbeitet werden könnten.

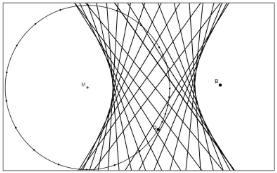
Achtung! Bei der Aufgabenstellung sollte man nicht nur einen Kreis und Punkt vorgeben, da sonst die Gefahr ungünstiger und unübersichtlicher Faltungen groß wäre. Durch die bereits in der Vorlage zusätzlich auf dem Kreis vorgegebenen Punkte erfolgt eine gezielte Vorauswahl, um ein besseres Gesamtergebnis zu unterstützen und nicht zielführende Faltvorgänge möglichst zu vermeiden. Sorgfältiges Falten und Nachzeichnen der Faltungen sind erforderlich, wenn man ansprechende Ergebnisse erzielen möchte⁶.

Weitergehende Vertiefungen (nur zur individuellen Förderung oder Projekte gedacht!)

Mit Aufgabe 6 können sich leistungsstarke SuS auch die vollständige algebraische Herleitung der Ellipsen- und Hyperbelgleichung in Mittelpunktslage aus der Brennpunkt-Defintion erarbeiten. Dabei könnten in Hinblick auf das 5-stündige Leistungsfach algebraische Kompetenzen gestärkt werden. Hier geht es konkret um die Umformung einer Wurzelgleichung, bei der zweimaliges Quadrieren erforderlich ist, die also auch nicht mehr im Kerncurriculum des Bildungsplans 2016 enthalten ist. Die Erarbeitung kann auch hier entweder durch Ergänzung und Begründung der nur teilweise vorgegebenen Umformungsschritte erfolgen oder aber einzelnen SuS im Rahmen eines differenzierenden Zusatzauftrags übertragen werden.

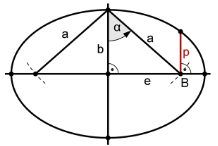
Mit Aufgabe 7 könnte man den Schlusspunkt setzen und unabhängig von Aufgabe 6 einige der Parametertransformationen in den Blick nehmen und vernetzen, die im Abschnitt 2.3. erläutert wurden. Inhaltlich werden dabei die Zusammenhänge zwischen den Halbmessern a und b, der linearen Exzentrizität e, dem Kegelschnittparameter p sowie der numerischen Exzentrizität ε erforscht. Zuvor muss allerdings die allgemeine Kegelschnittgleichung in Scheitelpunktslage bekannt sein (vgl. Material der 6. Stunde). In Aufgabe 7 wird die Ellipsengleichung aus der Mittelpunktslage durch eine Verschiebung parallel zur x-Achse in die Scheitelpunktslage überführt und mit der bekannten allgemeinen Kegelschnittsgleichung verglichen. Abschließend können im c)-Teil die verschiedenen algebraischen Zusammenhänge mit nebenstehender Skizze geometrisch visualisiert und gedeutet werden. Unter anderem könnte damit auch die zweite Grundvorstellung zur numerischen Exzentrizität entdeckt werden⁷. Im Erwartungshorizont finden Sie hierzu Erläuterungen.

 

Unterrichtsverlauf: Herunterladen [odt][4.8 MB]

Unterrichtsverlauf: Herunterladen [pdf][2.3 MB]

 

¹Das Applet findet man im Materialpaket unter M03_geo/6_GeoGebra-Ergaenzung oder kann es auf der GeoGebra-Seite im Buch "IMP10 für Lehrkräfte" unter https://www.geogebra.org/m/jfeewf5p abrufen.

²Im Artikel von Wittmann ([WITT], 2005) findet man hierzu weitere Informationen und Kopiervorlagen.

³Vgl. [HAFT2], 2017, Kap 7.7.1 "Krümmungskreise von Ellipse, Hyperbel und Parabel", S. 212 ff.zum Hintergrund auch [SCHE2], 2007, in Kap VI.2 Ellipsen: "Scheitelkrümmungskreise", S. 201

⁴In GeoGebra könnte man beide Hyperbeln mit den Befehlen H1:x^2/a^2-y^2/a^2=1 und H2:y=1/x zeichnen lassen und anschließend H1 mit einer Drehung um 45° um den Urspung auf H1 abbilden.(Vgl. [HAFT2], 2017, Kap. 7.2.1.1, S. 188)

⁵Hierzu wird auch auf die Beschreibung und Einordnung der Falt-Experimente im Unterrichtskonzept von Hubert Weller verwiesen ([WELL], 2009: Abschnitt "Falt-Experimente, Leitlinie und Leitkreis").AlleFaltaufgaben zu Hüllkurven von Parabel, Ellipse und Hyperbel sind auch kompakt in der Datei 2_kopiervorlagen/M10geo00_Vorlage_Gefaltete_Geraden.odtzusammengefasst.

⁶Falls Sie Interesse an den GeoGebra-Dateien zum Generieren der Vorlagen haben sollten, können diese gerne auf Anfrage (an olaf.grund@zsl-rska.de) zur Verfügung gestellt werden.

⁷Details zu den drei Kontexten der numerischen Exzentrizität in 2.5. und [HAFT2], Kap 7.2.2.1, S. 190

 

Weiter zu Hüllkurven und Leitkreise