Das Problem des kürzesten Weges – Dijkstra und die Ameisen
Graphen sind den SuS aus IMP-Mathematik Klasse 8 bereits geläufig. Voraussetzung für dieses Kapitel sind aber lediglich die Begriffe Knoten und Kante.
Als Einstieg eignet sich eine Straßenkarte, verbunden mit dem Auftrag, den kürzesten Weg von einem Ort zu einem anderen zu finden (siehe Präsentation). Dabei kann thematisiert werden:
- Die Länge der gezeichneten Straßen muss nicht der tatsächlichen Länge entsprechen.
- Der Graph kann als Modell der Wirklichkeit gesehen werden, und damit die Problemstellung weiter vereinfachen. Alle Dinge, die nicht zur Lösung des Problems notwendig sind, werden weggelassen. Wirklichkeit → Straßenkarte → Graph.
- Jede Straßenkarte kann als Graph gezeichnet werden. Dabei ist jede Straßenkreuzung als Knoten zu betrachten, auch wenn sich dort keine Ortschaft befindet.
- Die Suche nach dem kürzesten bzw. dem schnellsten Weg unterscheiden sich nicht. Der Unterschied liegt nur in der Einheit der Kantenbeschriftung (z.B. km, min).
Nachfolgend wird das Problem auf dem Arbeitsblatt strukturiert betrachtet.
In Aufgabe 1 wird der kürzeste Weg in zwei übersichtlichen Graphen gesucht. Die Frage, wie man sicher sein kann, dass es keinen kürzeren Weg gibt, lässt sich bei dem ersten Graphen einfach durch Aufschreiben aller möglichen Wege beantworten. Bei dem zweiten Graphen werden die meisten SuS argumentieren, dass ihr Weg der kürzeste sein muss. Falls einige Schüler nicht auf ABEF (12) kommen, sondern auf z.B. ADCF (15), ADCEF (14) oder ADEF (13), erkennen sie unmittelbar, wie leicht man vom eigenen Ergebnis überzeugt ist und dennoch falsch liegt. Bei diesem zweiten Graphen ist die Brute-Force-Methode, nämlich die Länge aller Wege zu ermitteln, sehr viel schwieriger, dennoch könnten sich manche SuS herausgefordert fühlen, alle Wege zu finden.
In Aufgabe 2 wird definiert, was genau die Brute-Force-Methode zum Finden des kürzesten Weges beinhaltet, nämlich:
Suche alle Wege, die bei A beginnen und die jeden Knoten höchstens einmal besuchen. Für jeden dieser Wege berechne die Entfernung von A bis F.
In Aufgabe 3 ermitteln die SuS nun die Anzahl aller möglichen Wege in einem vollständigen Graph, die bei A beginnen und bei Z enden:
3 Knoten:
2 Wege

4 Knoten:
Z kann über drei Wege erreicht werden:
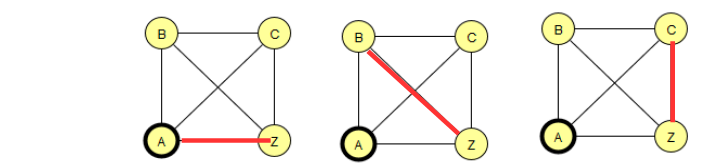
direkt von A, von B kommend, von C kommend.
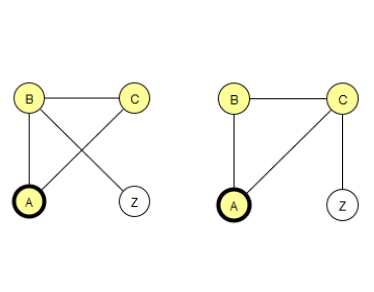
- Um von A nach Z zu gelangen, gibt es genau einen Weg.
- Um im Graph ABC von A nach B zu gelangen, gibt es 2 Wege.
- Um im Graph ABC von A nach C zu gelangen, gibt es 2 Wege.
Also gibt es 1+2+2 = 5 verschiedene Wege von A nach Z.
5 Knoten:
Z kann über 4 verschiedene Wege erreicht werden: Direkt von A aus, von B, von C, von D kommend.
- Um von A nach Z zu gelangen, gibt es genau einen Weg.
- Um im Graph ABCD von A nach B zu gelangen, gibt es 5 Wege.
- Um im Graph ABCD von A nach C zu gelangen, gibt es 5 Wege.
- Um im Graph ABCD von A nach D zu gelangen, gibt es 5 Wege.
Also gibt es 1+5+5+5 = 16 verschiedene Wege von A nach Z.
6 Knoten:
1+16+16+16+16 = 1+3•16 = 65 Wege
7 Knoten:
...
Bei 100 Koten sind es bereits 2,56•10154 verschiedene Wege.
In Deutschland gibt es zum Vergleich 10.848 Gemeinden (Stand 2019). Jeder Ort ist mit einigen Orten über Wege verbunden, aber nicht allen. Trotzdem ist leicht einsichtig, dass Zahl der möglichen Wege zwischen zwei Orten sehr groß sein kann und die Berechnung aller möglichen Wege (viel) zu lange dauert.
Die Brute-Force-Methode ist also grundsätzlich ein guter Ansatz, um mit Sicherheit den kürzesten Weg zu finden, aber in der Realität nicht geeignet, um z.B. in einem Navigationsgerät verwendet zu werden.
Bevor nun der Dijkstra-Algorithmus eingeführt wird, wird das Ameisen-Verhalten zum Finden des kürzesten Weges behandelt, das das Prinzip sehr anschaulich darstellt.1 Das bietet neben der Veranschaulichung eine Vernetzung mit der Biologie, sowie die Erkenntnis, dass Vorgänge, wenn sie in einen völlig anderen Bereich übertragen werden, zu erstaunlichen Ergebnissen führen können.
Wenn Ameisen von ihrem Bau zu einer Futterquelle laufen, dann laufen sie nach einer Weile auf dem kürzesten Weg. Sie zeigen dabei folgendes Verhalten: sie teilen sich auf und laufen vom Bau aus in alle möglichen Richtungen los. Kommen sie zu einem Abzweig, dann teilt sich der Trupp auf und in jede mögliche Richtung laufen Ameisen-Trupps weiter. So verfahren sie an jedem Knoten-Punkt, wenn mehrere Richtungen möglich sind. Kommen Ameisen zu einem Knoten-Punkt, an dem bereits Ameisen sind, dann wissen sie, dass die anderen Ameisen einen schnelleren Weg gefunden haben (und sie selber können umkehren). Treffen zwei Ameisentrupps aufeinander, während sie einen Weg entlanglaufen, so ist klar, dass dieser Weg aus beiden Richtungen betrachtet, ungeeignet ist, um schnell zum Ziel zu kommen. Beide Trupps können umkehren und einen anderen Weg suchen. Die Ameise, die als erste am Ziel ankommt, hat den kürzesten Weg gefunden.
Voraussetzung ist, dass es sehr viele Ameisen gibt, und dass sich alle gleich schnell bewegen.
Dieser 'Algorithmus' kommt der Realität sehr nahe. In der Natur markieren Ameisen ihre Wege mit Pheromonen. Auf einem sehr langen Weg kommen sie seltener entlang – weil sie dafür länger benötigen – und die Pheromon-Spur verfliegt schneller. Auf einem kurzen Weg, kommen Ameisen häufiger entlang, weil die Entfernung kürzer ist, deshalb ist die Pheromon-Spur intensiver.
Auf dem Arbeitsblatt sind die wesentlichen Elemente des Algorithmus aufgeschrieben. Die Fallunterscheidung, falls mehrere Trupps aufeinandertreffen notieren die SuS selber. Zunächst erweckt es den Eindruck, dass es drei verschiedene Fälle gibt: (1.) ein Trupp trifft, während er sich auf einem Weg befindet auf einen anderen. (3.) ein Trupp kommt zu einem Ort, an dem bereits Ameisen sind. (2.) Zwei Trupps kommen gleichzeitig an einem Ort an.
Der Fall 2, bei dem zwei Trupps gleichzeitig an einem Ort ankommen, bedeutet, dass beide Wege gleich schnell sind. Dann vereinen sich die beiden Trupps und teilen sich, wie ein einzelner Trupp, auf die verbleibenden Wege auf. Daher muss dieser Fall nicht gesondert betrachtet werden.
Der Fall 3 kann gar nicht auftreten (obwohl er zur Erklärung des Verhaltens als wesentlich erscheint). Wenn ein Trupp zu einem Ort kommt, dann teilt er sich auf und läuft auf allen möglichen Wegen weiter, also auch auf dem Weg, auf dem die langsameren Ameisen gerade anmarschieren, und damit handelt es sich um Fall 1.
In Aufgabe 3 simulieren die SuS das Ameisen-Verhalten Schritt für Schritt. Das kann zunächst gemeinsam an der Tafel begonnen werden und dann von den SuS selbstständig zu Ende geführt werden.
Die Frage, wie man das Ameisen-Verhalten in einen computertauglichen Algorithmus überführen kann, führt zum Dijkstra-Algorithmus.
Hinweis: Der Ameisen-Algorithmus ist nur zur Veranschaulichung gedacht, relevant ist der Dijkstra-Algorithmus.
Die SuS analysieren zunächst den vorgegebenen Algorithmus, indem sie ihn auf einen einfachen Graphen anwenden. Das kann gemeinsam an der Tafel erfolgen oder in Kleingruppen.
Hinweis:
Beim Übergang vom Ameisenverhalten zum Dijkstra-Algorithmus können einige Schüler Schwierigkeiten haben, weil die Algorithmen nicht exakt gleich sind: Die Ameisen laufen alle gleichzeitig. Es gibt sehr viele Ameisen, die gleichzeitig in alle Richtungen laufen. Der Dijkstra-Algorithmus hingegen wertet immer nur einen Knoten aus und bestimmt die Entfernungen zu den Nachbarknoten. Dabei kann es durchaus vorkommen, dass man zunächst zu große Zahlen bei einem Knoten einträgt. Das passiert bei den Ameisen nicht, da den Ameisen schon unterwegs andere Ameisen entgegenkommen. Daher tritt der Arbeitsschritt des Vergleichens mit den schon eingetragenen Werten und ggf. Anpassung des bisher besten Weges bei den Ameisen überhaupt nicht auf. Man kann der Verwirrung vorbeugen, indem man darauf hinweist, dass Dijkstras Algorithmus auf der prinzipiellen Idee des Ameisenverhaltens aufbaut, allerdings so gestaltet ist, dass er sinnvoll auf einem Computer ausgeführt werden kann. Eventuell kann man mit den SuS die Unterschiede zwischen beiden Algorithmen herausarbeiten.
Beide Algorithmen liefern eine Baum-Struktur, nachdem die unbrauchbaren Wege entfernt bzw. als unbrauchbar markiert wurden. Dieser Baum zeigt, beginnend bei der Wurzel (Startort), die kürzesten Wege zu allen anderen Orten.
Hinweise zum Dijkstra-Algorithmus:
Um die Darstellung möglichst überschaubar zu halten und Redundanz zu vermeiden, wurde bei der Beschreibung des Dijkstra-Algorithmus auf den Eintrag der unendlichen Entfernung an jedem Knoten zu Beginn verzichtet. Ebenso auf den Eintrag des jeweiligen Vorgänger-Knotens. Wenn man mehr Nähe zu der programmtechnischen Umsetzung herstellen möchte, kann man z.B. die relevanten Wege als Pfeil darstellen (gerichtete Kanten). Alternativ kann an jeden Knoten auch zusätzlich der Vorgängerknoten vermerkt werden.
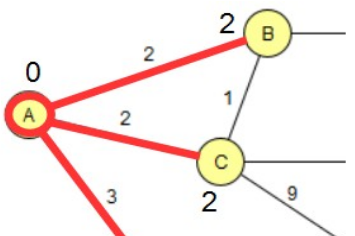
Haben mehrere Knoten dieselbe Entfernung, wählt man davon einen beliebigen als aktuellen Knoten. In der Abbildung kann man B oder C als nächsten aktuellen Knoten wählen.
Falls es mehrere kürzeste Wege gibt, findet der Algorithmus nur einen, nicht alle. Die Ameisen finden im Gegensatz dazu immer alle kürzesten Wege.
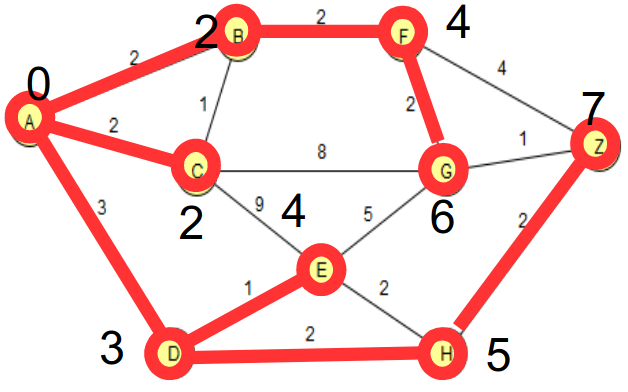
In der Abbildung ist A-D-H-Z (7) ist der gefundene kürzeste Weg zu Knoten Z. Der Weg A-B-F-G-Z (7) ist gleich kurz, wird aber nicht gefunden. (Siehe dazu Aufgabe 2 b.)
Grundsätzlich ist der Dijkstra-Algorithmus dann zu Ende, wenn es keine nichtmarkierten Knoten mehr gibt. Damit findet der Algorithmus die kürzesten Wege vom Start-Knoten zu allen anderen Knoten. Bei der Suche des kürzesten Weges vom Start zum Ziel, kann man den Dijkstra- Algorithmus vorzeitig beenden, nämlich sobald der aktuelle Knoten gleich dem Zielknoten ist.
Der Dijkstra-Algorithmus liefert nur dann den kürzesten Weg, wenn die die Kantengewichte positiv sind. Da die SuS wahrscheinlich nicht auf die Idee von negativen Kantengewichten kommen, muss das nicht weiter thematisiert werden.
In Aufgabe 2 stehen zwei Graphen zur Anwendung des Algorithmus zur Verfügung. Man kann zusätzlich die beiden Graphen des letzten Arbeitsblattes verwenden und damit ggf. Unterschiede zum Ameisenverhalten herausarbeiten. Ein zusätzlicher komplexerer Graph (2(c)) ist optional und etwas herausfordernd.
In Aufgabe 3 wird ein Straßennetz dargestellt, in dem 'Einbahnstraßen' enthalten sind.
Der Algorithmus kann wie gewohnt ausgeführt werden, es müssen lediglich die Richtungen der Pfeile beachtet werden.
Hinweis:
Bei gerichteten Graphen sind die Kanten als Pfeile dargestellt, die angeben, in welche Richtung die Beziehung gilt. Dies kann als 'Einbahnstraße' interpretiert werden. Gehen die Pfeile in beide Richtungen, gilt auch die Beziehung in beide Richtungen. Bei ungerichteten Graphen, gehen die Pfeile immer in beide Richtungen und werden daher weggelassen. Die Kante wird als Linie dargestellt. Als weitere Differenzierung kann die Darstellung eines gerichteten bzw. eines ungerichteten Graphen als Tabelle thematisiert werden.
In Aufgabe 4 werden kürzeste Wege übertragen auf Beziehungen in sozialen Netzwerken.
Die Aufgaben 5-7 stehen zur Differenzierung oder Ergänzung zur Verfügung.
In Aufgabe 5 wird in einem Tool des Lehrstuhls M9 der TU München der Dijkstra-Algorithmus Schritt für Schritt ausgeführt und erklärt2. Es sind leichte Kontrollfragen zu beantworten. Unter 'Weiteres' werden weitere Problemstellungen vertieft: Wie sieht der (Pseudo-)Code des Algorithmus aus? Wie schnell ist der Algorithmus? Berechnet der Algorithmus wirklich die kürzesten Wege? Wie löst man das Problem negativer Kantenkosten? Wo finde ich noch mehr Informationen zu Graphalgorithmen?
In Aufgabe 6 wird der A*-Algorithmus visualisiert. Zwischen Start und Ziel kann man zunächst ein vertikales Hindernis setzen und führt dann nacheinander den Dijkstra- und der A*-Algorithmus aus.3
In Aufgabe 7 kann der A*- Algorithmus von den SuS näher untersucht werden.4
Zusatzmaterial
Eine weitere Seite zum A*-Algorithmus:
http://www.geosimulation.de/methoden/a_stern_algorithmus.htm5
Sehr anschaulicher Vergleich von mehreren kürzester-Weg-Algorithmen:
https://www.redblobgames.com/pathfinding/a-star/introduction.html6
Tool zum Testen des Dijkstra-Algorithmus: Material → Software → Dijkstra.jar17
Tool zum Erstellen von Graphen: Material → Software → GraphEditor.jar
1 Dieses Vorgehen orientiert sich an Jens Gallenbacher: Abenteuer Informatik. Springer, Heidelberg, 2017
2 https://www-m9.ma.tum.de/graph-algorithms/spp-dijkstra/index_de.html (abgerufen am 28.04.19)
3 https://qiao.github.io/PathFinding.js/visual/ (abgerufen am 28.04.19)
4 https://www-m9.ma.tum.de/graph-algorithms/spp-a-star/index_de.html (abgerufen am 28.04.19)
5 Abgerufen am 28.04.19
6 Abgerufen am 28.04.19
7 Erstellt von Dirk Zechnal, Tom Schaller
Unterrichtsgang: Herunterladen [odt][1 MB]
Unterrichtsgang: Herunterladen [pdf][824 KB]
Weiter zu Kopiervorlagen
