Sie sind hier:

Grundsätzliches zur Konzeption

Im Mittelpunkt der Einheit stehen die Einführung und Begründung der Kreiswinkelsätze.
Da die Beweise der Sätze erst dann Sinn machen, wenn ihre Aussagen von den Schülerinnen und Schülern¹ wirklich verstanden worden ist, ergibt sich die Struktur der Einheit quasi von selbst, sie ist in folgende drei Unterrichtsphasen unterteilt:

1.+2. Stunde: Begründungsbasis aktivieren und Kreiswinkel erkunden
3.+4. Stunde: Kreiswinkelsätze verstehen und beweisen
5.+6. Stunde: Kreiswinkelsätze anwenden – Weitere Beweise

Nach der Aktivierung bekannter Sätze und Zusammenhänge aus Klasse 7 und 8 in der ersten Stunde, werden in der zweiten und dritten Stunde zunächst die neuen Begriffe im Kontext der Kreiswinkelsätze eingeführt und passende Vorstellungen entwickelt. Auf Basis einer ganzheitlich angelegten Erkundungsphase in der zweiten Stunde werden die Sätze in der dritten Stunde formuliert und bei ersten Anwendungen weiter durchdrungen. Erst danach folgt in der 4. Stunde die Erarbeitung eines formalen Beweises.
In den letzten beiden Stunden der Einheit können verschiedene Zusammenhänge im Kontext der Kreislehre erkundet und weitere Sätze bewiesen werden. Diese Phase eröffnet reichhaltige Anknüpfungspunkte, ist aber bewusst offen gehalten, so dass sie in der Praxis auf Basis des Materials sehr unterschiedlich ausgestaltet werden kann.

Ein wichtiges Ziel bei der Konzeption der ersten vier Stunden war neben dem Aufbau adäquater Vorstellungen auch die inhaltliche Vorentlastung des Beweises in der 4. Stunde. Die dazu erforderliche Begründungsbasis wird daher über die ersten drei Stunden hinweg aufgebaut.

Optionale Vertiefungen wie z.B. der Exkurs zur Konstruktion von Tangenten an den Kreis werden bei der Beschreibung der einzelnen Stunden erwähnt. Solche Vertiefungen gehen über die Vorgaben des Bildungsplans hinaus und sind als ergänzendes Angebot gedacht. Da sie ebenfalls binnendifferenzierend gestaltet sind, können sie entweder mit der gesamten Klasse oder als Zusatzaufträge für einzelne Schülergruppen genutzt werden.

Vorbemerkung zum Peripheriewinkelsatz – Ganzheitlicher Zugang

Bildquelle: ZPG IMP [CC BY-SA 3.0 DE]

In den verschiedenen Quellen gibt es keine einheitliche Auffassung über Inhalte und Bezeichnung des Peripheriewinkelsatzes.² Um die Zusammenhänge wirklich zu verstehen, ist es aus didaktischer Sicht angezeigt, einen ganzheitlichen Zugang zu wählen und auch den Sehnentangentenwinkel einzubeziehen. In der vorliegenden Einheit wurde daher eine Fassung zugrunde gelegt, die neben den Aussagen zum Umfangs- und Mittelpunktswinkel auch die Gleichheit von Umfangs- und Sehnentangentenwinkel enthält und sich in der konkreten Formulierung auf Kreisbogen statt Kreissehnen bezieht³:

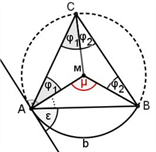
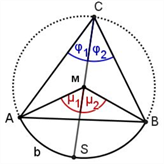
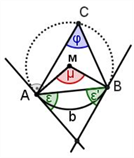
Peripheriewinkelsatz (Kreiswinkelsätze), vgl. Bild
Alle Umfangswinkel φ über einem Kreisbogen b sind gleich groß (UWS),
jeder ist halb so groß wie der zum Bogen b gehörige Mittelpunktswinkel μ (MWS)
und ebenso groß wie der zum Bogen b gehörige Sehnentangentenwinkel ε (STWS).

Die drei einzelnen Aussagen werden dabei in dieser Einheit als Umfangswinkelsatz (UWS), Mittelpunktswinkelsatz (MWS) und Sehnentangentenwinkelsatz (STWS) bezeichnet und im Sinne einer nachhaltigen Begriffsbildung ab der zweiten Stunde erkundet und beschrieben. In der 3. Stunde werden die drei Aussagen als eigenständige Sätze formuliert, wobei auch Formulierungen eingebunden sind, die sich auf Kreissehnen beziehen. Um dabei möglichen Fehlvorstellungen entgegenzuwirken, wird der Zusammenhang zwischen Kreissehnen, Bogen und Kreiswinkeln thematisiert. Erst in der 4. Stunde werden die drei Sätze dann unter dem Dach des Peripheriewinkelsatzes zusammengefasst und in der oben aufgeführten einfacheren Formulierung bewiesen. Die Bezeichnung Peripheriewinkelsatz wurde dabei von Scheid / Schwarz (a.a.O.) übernommen, um den Satz mit einem eigenen Begriff von den "Teilsätzen" abzugrenzen. Das Wort "Peripheriewinkelsatz" muss aber nicht zwingend im Unterricht verwendet werden. Falls man den SuS diesen weiteren Begriff ersparen möchte, kann man ihn auf dem Arbeitsblatt löschen und weiterhin von den Kreiswinkelsätzen sprechen. Tatsächlich taucht der Satz in der weiten Fassung (mit allen drei Aussagen) auch unter der Bezeichnung "Satz vom Umfangswinkel" oder auch "Sehnentangentenwinkelsatz" auf. Bei Wikipedia findet sich dazu beispielsweise folgende prägnante Formulierung⁴:

Die beiden Sehnentangentenwinkel eines Kreisbogens sind so groß
wie die zugehörigen Umfangswinkel (Peripheriewinkel) und
halb so groß wie der zugehörige Mittelpunktswinkel (Zentriwinkel).

Zur Rolle und zum Einsatz digitaler Werkzeuge

Dynamische Geometrie-Systeme (DGS) erlauben es durch (ggf. animierte) Visualisierungen von Zusammenhängen die Entwicklung tragfähiger Vorstellungen zu unterstützen, falls ihr Einsatz gut auf die Begriffsbildungsschritte abgestimmt ist und nicht zum falschen Zeitpunkt erfolgt. Der Einsatz sollte außerdem die Entwicklung von eigenen Vorstellungen der SuS anregen und darf dieser nicht vorgreifen bzw. diese nicht dominieren. Die Bedienkompetenzen der SuS sollten dabei nicht im Vordergrund stehen, können aber durchaus behutsam gefördert werden, so dass die SuS ein DGS ihrer Wahl für den weiteren Mathematikunterricht nutzen können.
Der Einsatz eines DGS ist im Bildungsplan für diese Einheit ausdrücklich gefordert, aber nicht explizit einer bestimmten Unterrichtsphase zugeordnet (siehe 3.2.2.3, (2)). In der zweiten und fünften Stunde sollten die Erkundungen idealerweise im Computerraum oder im Klassenzimmer mit Endgeräten stattfinden. Darüber hinaus sind in den einzelnen Stunden weitere Einsatzmöglichkeiten beschrieben. Die vorliegenden Arbeitsblätter wurden auf die frei verfügbare Software GeoGebra abgestimmt, können aber auch für andere DGS modifiziert werden.
Um die technische Organisation zu erleichtern, wurde begleitend ein GeoGebra-Buch für IMP 9 eingerichtet ⁵, in dem die Applets zentral abrufbar sind. Das direkte Abrufen aus dem Netz bringt den Vorteil mit sich, dass die Auflösung automatisch an die jeweiligen Endgeräte angepasst wird, erfordert allerdings eine Internetanbindung. Falls dies nicht möglich ist, können die Applets vorab heruntergeladen und intern im Netzwerk der Schule zur Verfügung gestellt werden, sofern die Software GeoGebra installiert ist. Alle Applets sind auch im Materialpaket unter M03_geo im Unterverzeichnis 3_vorlagen_tauschordner bzw. 5_praesentationen abrufbar.

Hinweise zur Dokumentation – "Zweispaltenbeweise"

Beweisen und Argumentieren sind zentrale Kompetenzen, bei denen auch die Frage der Ergebnissicherung entscheidend ist. Eine praktikable, angemessene Dokumentation muss eingeführt und eingeübt werden. An einigen Stellen der Einheit wurde dazu das Prinzip der Zweispaltenbeweise eingebunden. Es sieht ein dreischrittiges Vorgehen vor, um die Kompetenz des Beweisens altersangemessen zu unterstützen⁶:

Schritt: Klare Trennung von Voraussetzung und Behauptung
Schritt: Skizzieren einer Beweisfigur mit allen wichtigen Größen und ggf. Hilfsgrößen/ -linien
Schritt: Aus den Voraussetzungen und bekannten Zusammenhängen wird die Behauptung schrittweise hergeleitet. Dies wird übersichtlich in zwei Spalten dokumentiert.

Der Anfang des Beweises des Satz des Thales könnte dann z.B. so aussehen:

Beweisschritt	Begründung
(1)	γ₁+γ₂=γ	Hilfslinie teilt γ in γ₁und γ₂
(2)	MA=MC	MA und MC sind Radien des Kreises
(3)	γ₁=α	Basiswinkel im gleichschenkligen Dreieck sind gleich groß
...	...	...

Zur Entwicklung von Beweiskompetenzen kann außerdem die "Zwei-Tore-Regel" hilfreich sein, die hier nur kurz skizziert werden soll. Für weitergehende Informationen wird auf die übersichtliche Zusammenfassung von Herrn Brockmann-Behnsen verwiesen⁷.

Man stellt sich dabei zwei Tore vor, die bei jedem Beweisschritt passiert werden müssen.
Jedes Tor wird von einem Wächter bewacht, der eine Leitfrage stellt:

TOR 2	TOR 1
Nutzen des geplanten Schrittes	Begründung für den geplanten Schritt
Wächter 2: Was bringt es dir?	Wächter 1: Warum darfst du das?

Nur wenn man dem strengen ersten Wächter eine gute Begründung für die Rechtmäßigkeit des geplanten Schrittes liefern kann, darf man zum zweiten Tor weitergehen. Dort möchte der freundliche zweite Wächter helfen, unnötige Schritte und Arbeit zu vermeiden.

Die Tore sind hier von rechts nach links angeordnet, um den Zusammenhang mit dem Prinzip des Zweispaltenbeweises zu verdeutlichen. Die Antwort auf die erste Frage muss für jeden Beweisschritt jeweils in der rechten Spalte begründet werden (horizontale Sicht). Die zweite Frage nach dem Nutzen eines geplanten Beweisschrittes nimmt in der linken Spalte die Abfolge der Argumentation im Gesamtzusammenhang in den Blick und hat das Ziel, mit möglichst wenigen, übersichtlichen Schritten auszukommen (vertikale Sicht).

Beweisvarianten der Kreiswinkelsätze

Für die vollständige Beweisführung müssen verschiedene Fälle betrachtet werden.
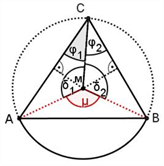
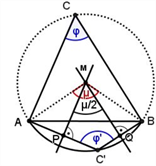
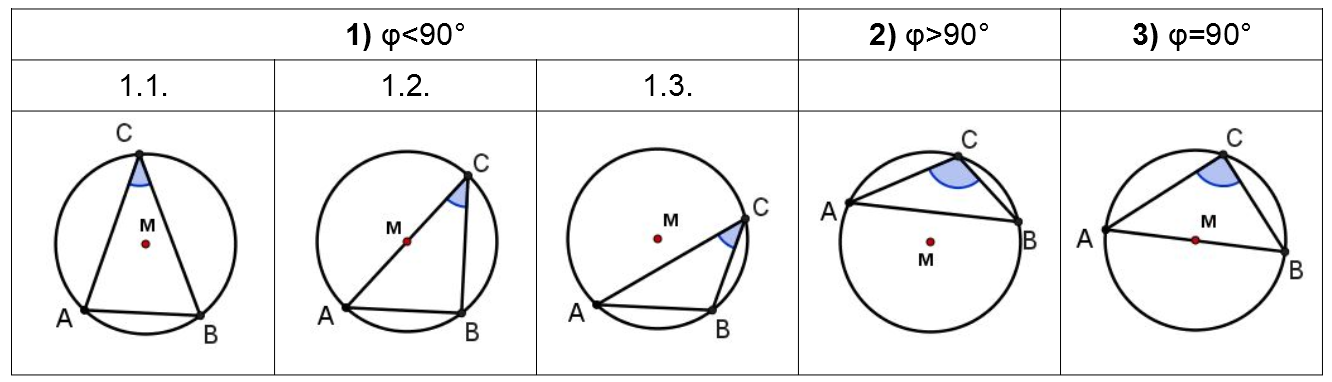
Im vorliegenden Unterrichtsvorschlag werden nach der Größe des Umfangswinkels φ bei C und der Form des Dreiecks ABC folgende Fälle unterschieden:

Bildquelle: ZPG IMP [CC BY-SA 3.0 DE]

Dabei wurde der Spezialfall zum Satz des Thales als Fall 3) ans Ende gestellt, da er in der 4. Stunde von den SuS im Rahmen eines kurzen Auftrags eingeordnet wird und hierzu auf dem Arbeitsblatt keine Grafik eingebunden wurde. Die Unterfälle zu Fall 1) wurden anhand der Lage des Umkreismitttelpunkts M unterschieden:
1.1. M im Dreieck ABC.
1.2. M liegt auf der Seite AC (oder der Seite BC) des Dreiecks ABC.
1.3. M liegt außerhalb des Dreiecks ABC.

Bei Fall 1.3. wurde auf dem Arbeitsblatt darauf verzichtet, weiter zu unterscheiden.
Die Beweisführung ist beim Material der 4. Stunde ausführlich dokumentiert.

Abschließend sollen hier noch ausgewählte alternative Beweisideen aufgeführt werden, um die Vielfalt anzudeuten und Anknüpfungspunkte für Zusatzaufträge aufzuzeigen (GFS, …):

Beweisidee 1, [SCHE], 2007, S.39 Beweisgang ohne Verwendung des Außenwinkelsatzes (AWS) bei Betrachtung des Vollwinkels im Kreismittelpunkt: μ+(180°−2φ₁)+(180°−2φ₂)=360° → φ=φ₁+φ₂=μ/2 ε+(180°−μ)=90° → ε=μ/2, insbesondere ε= φ Dieses Vorgehen bietet sich an, falls der AWS nicht behandelt werden soll. Hinweis: Der Beweis wird für die Fälle 1.1) und 3) geführt. Die Fälle 1.3) und 2) werden in der Übungsaufgabe 1 behandelt, der Fall 1.2) wird nicht explizit aufgeführt.
Beweisidee 2, [SCHM], 1997, S. 173, ähnlich wie Idee 1 Diese Variante kommt bei der Argumentation mit Symmetrieüberlegungen, der Winkelsumme im Dreieck und dem Ergänzungswinkel am Vollkreis aus und könnte daher auch gut im Unterricht als Alternativbeweis entwickelt werden. Die Beweisfigur bleibt dabei noch relativ übersichtlich. φ₁=90°−δ₁/2 bzw. φ₂=90°−δ₂/2 φ₁+φ₂=180°−(δ₁+δ₂)/2 = [360°−(δ₁+δ₂)] / 2 = μ/2 Hinweis: Der Satz wird im Buch nur für den Fall 1.1. bewiesen.
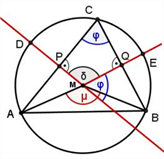
Beweisidee 3, [HALB], 2016, S.9/10 Für das Dreieck ABC wird die Gleichheit von Umfangswinkel φ im Punkt C und dem Sehnentangentenwinkel ε in Punkt A bzw. B direkt über die gestreckten Winkel an den Tangenten in den Punkten A, B und C hergeleitet. Das aus den drei Bedingungen resultierende Gleichungssystem führt zusammen mit der Winkelsumme im Dreieck ABC auf die Beziehung ε=φ. Anschließend wird für den Fall 1.1 gezeigt, dass φ=μ/2 gilt Hinweis: Die Fallunterscheidung ist hier nicht erforderlich, da ε=φ zuvor für alle Dreiecke bewiesen wurde.
Beweisidee 4, [KRAT], 1993, S. 110 Zuerst wird der "Winkelsatz für Sehnenvierecke" bewiesen (In einem Sehnenviereck ergänzen sich gegenüberliegende Winkel zu 180°), aus dem dann der MWS gefolgert werden kann. Dazu verwendet man neben dem Sehnenviereck AC‘BC über der Sehne AB ein zweites Viereck MPC‘Q. P bzw. Q sind die Mittelpunkte der Strecken AC‘ bzw. C‘B. Die Argumentation geht dann von den Mittelsenkrechten der Strecken AC‘ und C‘B aus, die aus dem Mittelpunktswinkel μ einen Winkel halber Weite "ausschneiden". Hinweis: In dieser Einheit wurde der umgekehrte (für die SuS leichter nachvollziehbare) Weg gewählt und der Winkelsatz für Sehnenvierecke aus dem Peripheriewinkelsatz gefolgert.⁸
Beweisidee 5, [SCHW], 1981, S. 88 Bei dieser Variante wird mit den beiden Mittelsenkrechten zu den Dreiecksseiten AC und BC argumentiert. Es gilt zunächst δ=180°−φ (folgt aus der Winkelsumme im Viereck PMQC). Daher hat auch der Nebenwinkel von δ die Winkelweite φ. E bzw. D liegen auf den Mittelsenkrechten der Sehnen BC bzw. CA und halbieren daher auch die Bogen BC bzw. CA. Deshalb beträgt der zum Bogen BA zugehörige Mittelpunktswinkel 2δ und es folgt μ=360°−2δ =360°−2(180°−φ)=2φ Hinweis: Im Lehrbuch wird auch der Fall 1.3) mit Beweisfigur behandelt, der Fall 1.2) wird als Übungsaufgabe empfohlen.
Beweisidee 6, ohne Quelle Eine elegante Rückführung des Falles 1.1) auf den Fall 1.2) (!) gelingt, wenn man wie im Bild den sogenannten "Südpol" S einzeichnet und den bewiesenen Spezialfall 1.2) auf die Umfangswinkel über den Bogen AS und SB anwendet. Da die Aussage nach Fall 1.2) für jedes Teilwinkelpaar φ₁ und μ₁ bzw. φ₂ und μ₂ gilt, muss sie auch für die zusammengesetzten Winkel φ=φ₁+φ₂ bzw. μ=μ₁+μ₂ gelten. Analog kann dann auch bei den Winkeldifferenzen im Fall 1.3) argumentiert werden.

¹Schülerinnen und Schüler wird im Folgenden SuS abgekürzt.

²Er wird auch als Umfangswinkel- oder Mittelpunktswinkelsatz bezeichnet und kann inhaltlich enger oder weiter gefasst sein. Seine Formulierung kann sich auf Kreissehnen oder Kreisbogen beziehen.

³Die Formulierung wurde (bis auf einzelne Fachbegriffe) aus [SCHE], 2007, S.39, übernommen

⁴Wikipedia: "Kreiswinkel", URL: https://de.wikipedia.org/wiki/Kreiswinkel , abgerufen am 23.4.2019

⁵Die Applets der Geometrieeinheit sind für SuS unter https://ggbm.at/k7u4ab9v abrufbar. Ergänzende Applets für Lehrkräfte findet man in einem zweiten GeoGebra-Buch unter https://ggbm.at/vz4vt4bw.

⁶nach [LENG], "Mathematik Neue Wege 4 – Arbeitsbuch für Gymnasien BW", Schroedel, 2006, S. 76

⁷Dort wird das Prinzip vorgestellt und exemplarisch beim Beweis des Satz des Thales angewendet.
Die Grundidee geht auf amerikanische Didaktiker zurück und wurde 2012 von Dirk Brockmann-Behnsen aufgearbeitet und weiterentwickelt. Die Zusammenfassung des Konzepts kann bei der Deutschen Nationalbibliothek online abgerufen werden: "Zwei-Tore-Regel und Zwei-Spalten-Beweis", BzMU13, 2012 (pdf) , https://d-nb.info/1105564797/34, abgerufen am 22.4.2019

⁸Der Beweisgang für den "Winkelsatz für Sehnenvierecke" ohne Verwendung der Kreiswinkelsätze ist bei den Erläuterungen zu Aufgabe 3 der fünften Stunde dokumentiert.

Unterrichtsgang: Herunterladen [odt][3 MB]

Unterrichtsgang: Herunterladen [pdf][3 MB]

Weiter zu Unterrichtsverlauf