Sie sind hier:

Zahldarstellung

Einführung

Im Mathematikunterricht erarbeitet man sich von der Grundschule ausgehend schrittweise die verschiedenen Zahlbereiche. Angefangen mit den natürlichen Zahlen ℕ , geht man über die ganzen Zahlen ℤ zu den rationalen Zahlen ℚ bis man schließlich bei den reellen Zahlen ℝ landet.

Vernachlässigt man die Tatsache, dass mit dem Computer natürlich nur eine beschränkte Zahlmenge darstellen lässt, so lassen sich diese Schritte mit ein paar Einschränkungen auch auf die binäre Darstellung im Computer übertragen und die unterschiedlichen Zahldarstellungen ähnlich zu den Zahlbereichserweiterungen im Unterricht behandeln.

Der Fokus liegt dabei auf der im Bildungsplan neu hinzugekommenen Festkommadarstellung. Es soll hier aber gezeigt werden, dass die Rechenverfahren die den unterschiedlichen Darstellungen (bis auf die Gleitkommadarstellung) gleich ist.

Computerdarstellung von ℕ : Binärsystem

Es soll hier nicht detailliert auf das Binärsystem eingegangen werden, es wird vorausgesetzt, dass man als Informatiker prinzipiell mit dem Binärsystem vertraut ist.

Zunächst sollte jedem klar sein, dass im Computer – anders als in der Mathematik – die Zahlmengen natürlich nicht unendlich sondern durch die Bitzahl begrenzt sind.

Im Aufbaukurs Informatik in Klasse 7 lernt man die einfache Binärdarstellung kennen, diese entspricht den natürlichen Zahlen. Meistens wird hierbei in der Schule auch das schriftliche Rechnen mit Binärzahlen analog zum Rechnen mit Dezimalzahlen eingeführt, welches die Schüler bereits in der Grundschule gelernt hatten.

Beispiele:

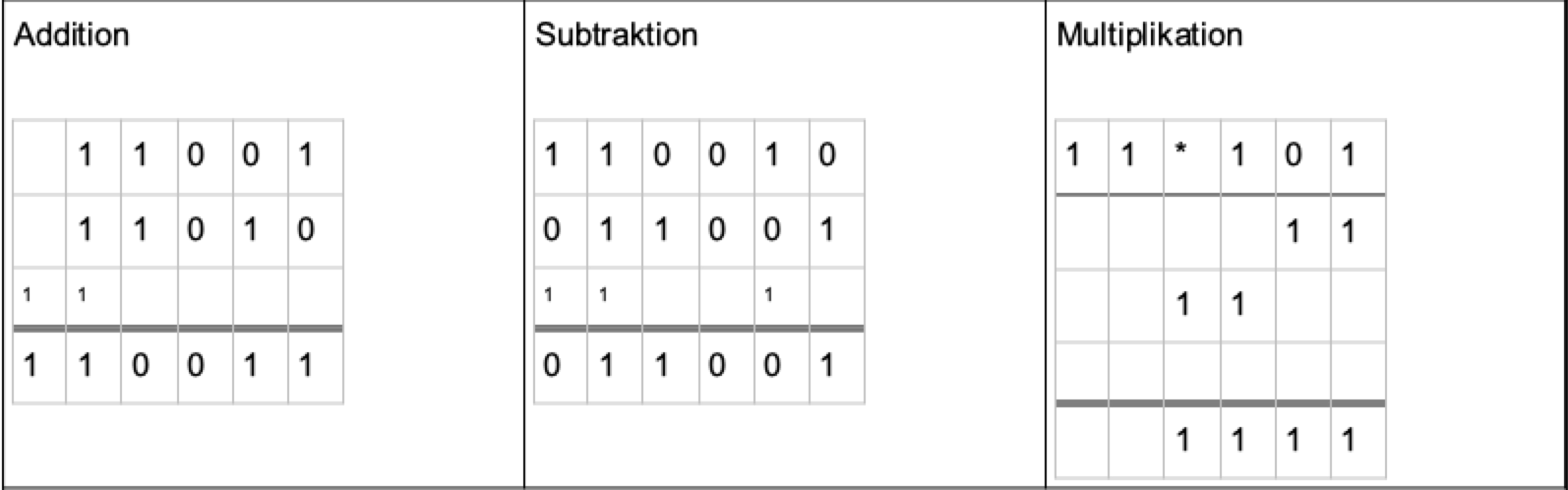
Bildquelle: Rechnen mit Binärzahlen von ZPG Informatik [CC BY-SA 4.0 DE], aus 1_hintergrund.odt, bearbeitet

Computerdarstellung von ℤ : Einer- und Zweierkomplement

Für die erste Zahlbereichserweiterung, den negativen Zahlen, lassen sich mehrere Darstellungen finden. Die für die Schüler am offensichtlichste ist, das erste Bit als Vorzeichenbit zu nutzen.

Beispiel: 13₁₀ = 0000 1101₂, − 13₁₀ = 1000 1101₂

Hiermit lassen sich allerdings die schriftlichen Rechengesetze nicht mehr anwenden.

Beispiel: − 13₁₀ + 1₁₀ = 1000 1101₂ + 0000 0001₂ = 1000 1110₂ = − 14₁₀ Widerspruch

Oftmals wird deshalb das sogenannte Einerkomplement benutzt. Bei diesem werden von allen „Zahlbits“ das Komplement gebildet.

Beispiel: 13₁₀ = 0000 1101₂, − 13₁₀ = 1111 0010₂

Mit Zahlen in diesem Einerkomplement lässt sich dann wie bisher rechnen, sofern die Rechnung nicht „über die Null“ geht. Ein damit zusammenhängendes Problem ist die doppelte Darstellung der Null (0₁₀ = 0000 0000₂ = 1111 1111₂).

Diese Probleme bei der Darstellung negativer Zahlen behebt das Zweierkomplement. Bei diesem wird lediglich die Wertigkeit des höchsten Bit negiert, so dass dieses bei einer 8-Bit-Zahl nicht dem dezimalen Wert 128 sondern − 128 entspricht.

Beispiele: 127₁₀ = 0111 1111₂
− 128₁₀ = 1000 0000₂
− 127₁₀ = 1000 0001₂
− 1₁₀ = 1111 1111₂

Auch wenn dieses auf den ersten Blick umständlich scheint, bietet diese Darstellung den Vorteil, dass sämtliche Rechnungen wie auch für die positiven Zahlen gelten! Man kann diese Rechnungen also auf der selben ALU des Prozessors durchführen.

Computerdarstellung von ℚ :Festkommazahlen

Die nächste Zahlbereichserweiterung, ist zugleich auch die Neuerung im Bildungsplan: die Einführung von Festkommazahlen. Bei so einer Zahl ist die Position des Kommas fest vorgegeben.

Anmerkung: Aus mathematischer Sicht ist die Festkommadarstellung natürlich keine exakte Darstellung von ℚ ! Das Vorgehen soll nur verdeutlichen, dass man didaktisch die Zahlbereichserweiterungen in der Informatik ähnlich zu denen in der Mathematik aufbauen kann.

Der Grundgedanke hinter Festkommazahlen ist die exakte Darstellung ohne Rundungsfehler einer Teilmenge der rationalen Zahlen. Dies gilt natürlich nur im Rahmen der Anzahl der Bits.

Beispiele: 4,7510 = 0001 0011₂, dabei setzt sich die Binärzahl aus 6 Vorkomma-, und 2 Nachkommastellen zusammen.

Man bezeichnet die Gesamtzahl der Bits mit n, üblicherweise sind dann die ersten k (≤ n) Stellen Vorkommastellen und die restlichen m (= n − k) Nachkommastellen.

Formal ist eine Festkommazahl wie auch eine Binärzahl definiert:

der Unterschied hierbei ist lediglich, dass der Exponent entsprechend auch in den negativen Bereich reicht.

Die Vorteile im schulischen Bereich sind folgende:

die Wertigkeit der Bits lassen sich analog zu den Zweierpotenzen fortsetzen:

Wertigkeit	32	16	8	4	2	1	0,5	0,25
Zweierpotenz	2⁵	2⁴	2³	2²	2¹	2⁰	2^− 1	2^− 2
Ziffern	0	0	0	1	0	0	1	1

Die Addition und die Subtraktion lassen sich identisch mit oben aufgeführten Rechenregeln durchführen.
Dementsprechend lassen diese sich auch auf einer herkömmlichen ALU berechnen.

Die Nachteile sind:

Der Zahlumfang ist relativ gering.
Bei Multiplikation und Division müssen die Stellen angepasst werden. (s.u.)
Nachkommastellen nicht beliebig darstellbar, z.B. lässt sich 0,1 nicht mit einer Festkommadarstellung ausdrücken.³

Aufgrund der exakten Darstellung ist die Menge aller Festkommazahlen einer vorgegebenen Länge n im Vergleich zu den Gleitkommazahlen sehr gering.

In der allgemeinen Nomenklatur werden Festkommazahlen mit einer Nachkommastelle mit „Q1“, mit zwei Nachkommastellen mit „Q2“ usw. bezeichnet.

Anpassung der Stellen: Werden zwei 8bit-Zahlen miteinander multipliziert, so ergibt sich daraus eine 16bit-Zahl. Bei dem bekannten, ganzzahligen Binärsystem werden die höchstwertigsten Bits einfach abgeschnitten, da diese nicht in einer 8bit-Zahl abgespeichert werden können. Selbiges gilt auch für Festkommazahlen, auch hier bräuchte man zur genauen Speicherung dann die doppelte Anzahl an Bits und wir müssen einen Teil davon abschneiden.

Werden zwei Q2-Zahlen miteinander multipliziert, so ergibt sich daraus eine Q4-Zahl. Dies lässt sich direkt an den Zweierpotenzen ablesen, hierfür muss man lediglich die niederwertigsten Stellen betrachten:
2⁻² · 2⁻² = 2⁻⁴ Daraus ergibt sich, dass man nach der Multiplikation, um wieder eine Q2-Zahl zu bekommen, entsprechend die letzten beiden Stellen (2⁻³ und 2⁻⁴) sowie die höchstwertigen 6 Stellen abschneiden muss, so dass auch wieder 8 Bit übrig bleiben.

Beispiele: (zum besseren Verständnis wird auch im Binärsystem hier das Komma mitgeschrieben)

17,75₁₀ = 010001,11₂
42,25₁₀ = 101010,01₂
17,75₁₀⋅42,25₁₀ = 749,9375₁₀ = 1011101101,1111₂
101101,11₂ = 45,75₁₀

Die 8 fett markierten Stellen ergeben die neue 8 Bit große Festkommazahl.

Des weiteren lassen sich damit nur Vielfache von 2er-Potenzen darstellen. Es lassen sich somit bestimmte Zahlen aus dem Dezimalsystem nur ungenau darstellen, insbesondere bei geringer Bitlänge.⁴

Computerdarstellung von ℝ : Gleitkommazahlen

Nicht im Bildungsplan enthalten sind die Gleitkommazahlen. Der Vollständigkeit halber sollen diese hier jedoch auch mit aufgeführt werden.

Wir betrachten zunächst die wissenschaftliche Darstellung von (insbesondere großen) Zahlen:

3,84 = 384 · 10⁻² = 38,4 · 10⁻¹ = 0,0384 ·10²

gesucht ist für die Darstellung im Computer, die:

einen möglichst großen Bereich der reellen Zahlen umfasst
die Genauigkeit bei kleinen Zahlen soll groß, bei großen Zahlen kann sie niedriger sein.

Die Gleitkommadarstellung arbeitet hier wie die wissenschaftliche Darstellung, eine Gleitkommazahl besteht aus mehreren Teilen:

einem Vorzeichenbit V
dem Exponenten E → Im hier dargestellten Standard IEEE754 mit einem 8 Bit langen Exponenten wird der Binärwert anschließend −127 gerechnet um den Exponenten zu bekommen.
der Mantisse M → Das ergibt die Nachkommastellen, als Vorkommastelle steht laut Definition immer 1.

Der eigentliche Zahlwert Z ergibt sich damit:
Z=(1+M) · 2^E-127

Anmerkung: man könnte auch eine andere Basis außer 2 benutzen, diese ist so aber im Standard IEEE754 definiert.

Beispiel: bei Java verwendet eine Variable vom Datentyp float 32 Bit, die sich wie folgt aufteilen: Vorzeichen (1 Bit), Exponent (8 Bit), Mantisse (23 Bit)

Bildquelle: Gleitkommadarstellung von ZPG Informatik [CC BY-SA 4.0 DE], aus 1_hintergrund.odt, bearbeitet

Es ergibt sich die Zahl Z = (1+0,625) · 2^{130 - 127} = 1,625 · 2³ = 13

Anmerkung: Die Multiplikation von Gleitkommazahlen ist aufwändiger als bei Festkommazahlen, die Addition sogar wesentlich aufwändiger! Deshalb enthalten moderne Prozessoren neben der ALU für Festkommaoperationen meist noch eine FPU (floating point unit), die auf Gleitkommaoperationen spezialisiert ist.

Um zwei Zahlen in Exponentendarstellung miteinander multiplizieren zu können, müssen Potenzgesetze angewendet werden. Dazu müssen lediglich die beiden Mantissen miteinander multipliziert und die Exponenten addiert werden.

Um zwei Potenzen addieren zu können, muss sowohl die Basis als auch der Exponent übereinstimmen. Die Basis ist hierbei immer 2, die Exponenten unterschieden sich jedoch im allgemeinen. Das bedeutet, dass für eine einfache Addition die beiden Zahlen zuerst umgerechnet werden müssen.

³ Auch in anderen Zahldarstellungen ist das nicht genau möglich!

⁴ Das selbe Problem hat natürlich auch die Gleitkommadarstellung, kann dort jedoch deutlich genauer angenähert werden.

Hintergrundinformationen: Herunterladen [odt][1 MB]

Weiter zu Textdarstellung

Zahldar­stel­lung

Ein­füh­rung

Com­pu­ter­dar­stel­lung von ℕ : Bi­närs­ys­tem

Com­pu­ter­dar­stel­lung von ℤ : Einer- und Zwei­er­kom­ple­ment

Com­pu­ter­dar­stel­lung von ℚ :Fest­kom­ma­zah­len

Computerdar­stellung von ℝ : Gleit­kom­ma­zah­len