Algorithmen mit optimaler Lösung
So vielfältig wie die Probleme sind auch die Lösungsansätze. Es gibt eine Vielzahl von Standardalgorithmen zur Lösung typischer Graphenprobleme. Grundsätzlich muss man dabei unterscheiden, ob das Ziel ist, die perfekte/beste Lösung zu finden oder ob es ausreichend ist, eine gute Näherungslösung zu finden. In vielen Fällen kann die beste Lösung nicht ermittelt werden, da der Zeitbedarf zu groß wäre (siehe Kapitel Laufzeitverhalten).
Tiefensuche / Breitensuche
Tiefen- und Breitensuche taucht im Bildungsplan im Zusammenhang mit Bäumen und mit Graphen auf. Da Bäume spezielle Graphen sind, lässt sich die Tiefen- bzw. Breitensuche von Graphen auch auf Bäume anwenden. In der Schule wird man aber vermutlich zunächst Bäume behandeln und erst danach die Graphen. Damit müssen die Algorithmen von Bäumen auf Graphen erweitert werden. Die Beschreibung der Algorithmen auf Bäumen finden Sie im Hintergrund zu den ADTs im Kapitel Bäume.
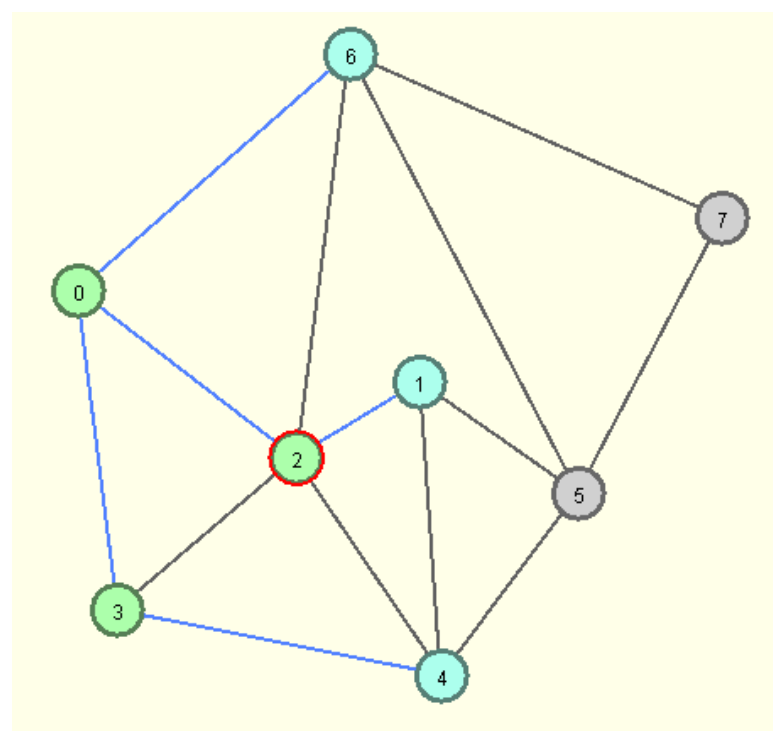
Breitensuche (eigenes Werk):
grün = fertig bearbeitet, türkis = in toDo-Liste
Bei der Bearbeitung des Knoten 2 durften der Knoten 3 (schon bearbeitet) und die Knoten 4 und 6 (schon in toDo-Liste) der toDo-Liste nicht hinzugefügt werden.
ZPG Informatik
[CC BY-SA 4.0 DE],
aus
1_graphen_hintergrund.odt
Überträgt man diese Algorithmen auf allgemeine Graphen, treten zwei Probleme auf:
- Es gibt in einem Graphen keinen ausgezeichneten Knoten, der der Wurzel des Baumes entspricht. Man beginnt die Algorithmen mit einem beliebigen Startknoten (hier Knoten 0).
- Aufgrund der Zyklen im Graphen kann man bei der Abarbeitung auf Knoten stoßen kann, die schon bearbeitet oder zumindest der toDo-Liste hinzugefügt wurden. Man kann bei der Tiefensuche sogar bis zurück zum Startknoten gelangen. Das ist bei Bäumen nicht möglich. Damit diese Knoten nicht erneut bearbeitet oder mehrfach der toDo-Liste hinzugefügt werden, kennzeichnet man sie als schon besucht.
Breitensuche kann man also gut mit dem ADT Schlange, Tiefensuche mit dem ADT Stapel realisieren. Tiefensuche lässt sich außerdem gut rekursiv implementieren, indem der Bearbeitungsalgorithmus mit dem als nächstes auszuwertenden Knoten erneut aufgerufen wird. Erst nach Rückkehr von der Rekursion wird der nächste Nachbarknoten bearbeitet. Sucht man in einem Graphen also nach einem Knoten, der eine bestimmte Bedingung erfüllt (Attribut(k) ist wahr), ergeben sich nebenstehende Pseudocodes für die Tiefen- und Breitensuche:

Code für Tiefensuche und Breitensuche
ZPG Informatik
[CC BY-SA 4.0 DE],
aus
1_graphen_hintergrund.odt
Achtung: Man muss bei der Implementierung der Algorithmen immer beachten, ob es sich um einen gerichteten oder ungerichteten Graphen handelt.
Beispiele für Algorithmen:
Breitensuche:
Zyklensuche, Algorithmus A von Moore, Dijkstra (wobei Knoten in einer Prioritätsschlange gespeichert werden), Zusammenhang eines Graphen
Tiefensuche:
Zusammenhang eines Graphen, Zyklensuche
Backtracking (Brute-Force-Ansatz)
Ein grundsätzlicher Lösungsansatz, der für sehr viele Problemstellungen anwendbar ist, ist das Backtracking. Im Bildungsplan des Leistungsfachs findet es sich unter 3.3.2.3 Rekursion (6) "das Prinzip des Backtrackings anhand einer geeigneten Problemstellung (zum Beispiel Acht-Damen-Problem, Magische Quadrate, Zyklensuche) erläutern". Mit dem Beispiel "Zyklensuche" ist der Bezug zu den Graphen auch im Bildungsplan hergestellt.
Backtracking liefert immer die perfekte/beste Lösung eines Problems. Backtracking ist im Prinzip systematisches Probieren aller Möglichkeiten ("Brute Force"). Wenn es für eine endliche Zahl von Entscheidungen jeweils endlich viele Möglichkeiten gibt, kann man für jede Entscheidung der Reihe nach alle Varianten durchprobieren. Dies ist bei den Graphenproblemen nahezu immer der Fall. Entweder wird für jeden Knoten eine Entscheidung getroffen (z.B. welchen Weg man weitergeht, ob er zu einer Teilmenge dazugehören soll oder nicht oder in welcher Farbe einer vorgegebenen Farbpalette er gefärbt werden soll) oder für jede Kante (soll sie zum Minimal Spanning Tree dazugehören oder nicht, gehört sie zu einem Weg oder nicht).
Beim Backtracking wird also z.B. mit einem Startknoten begonnen und die erste Entscheidung getroffen. Hierfür wählt man die erste Möglichkeit (z.B. Knoten 1 bekommt Farbe 1). Danach geht man zum nächsten Knoten und trifft dort die Entscheidung. Auch hier probiert man systematisch alle Möglichkeiten durch (z.B. Farbe 1 ist bei Knoten 2 nicht erlaubt, daher wird Farbe 2 probiert). Sobald man eine zulässige Möglichkeit gefunden hat, geht man zur dritten Entscheidung über. Sollte es gar keine zulässige Möglichkeit mehr geben, geht man einen Schritt zurück (daher der Name des Lösungsansatzes) und probiert dort die nächste Möglichkeit. Hat man für den ganzen Graphen zulässige Entscheidungen getroffen, dann ist die Lösung des Problems gefunden.
Sucht man bei einem Optimierungsproblem die beste Lösung und nicht nur irgendeine, darf man das Verfahren nicht abbrechen, sobald man eine Lösung gefunden hat, sondern muss alle Lösungen bestimmen und sich die bis dahin beste Lösung merken.
Wichtig ist dabei nur, dass in der Entscheidungsfolge jeder Knoten/Kante maximal einmal vorkommen darf, da sonst unendlich viele Entscheidungen notwendig sein könnten. Eine Tiefensuche würde dann unendlich weitergehen. Daher ist es bei Graphen oft sinnvoll, die Knoten als "besucht" zu kennzeichnen, um zu wissen, welche Knoten schon ausgewertet wurden.
Backtracking kann man sehr gut rekursiv implementieren. Für jeden Entscheidungsschritt ruft sich der Backtrackingalgorithmus rekursiv auf. Bei Graphenalgorithmen wäre der Zustand z der Zustand des Graphen, also die Knotenwerte und die Markierungen der Knoten und Kanten: public Zustand loese(Zustand z) {
aktuellerZustand = z;
if (z.istErkennbarFalsch()) {
return null;
}
if (z.istZielzustand()) {
return z;
}
for (int i=0; i< z.getAnzahlMoeglichkeiten(); i++ ) {
Zustand z2 = z.erzeugeKopie();
z2.waehleMoeglichkeit(i);
Zustand erg = loese(z2);
if (erg != null) {
return erg;
}
}
return null;
}
Eine gute Darstellung des Backtracking-Prinzips findet man beim Matheprisma der Uni Wuppertal unter http://www.matheprisma.uni-wuppertal.de/Module/BackTr/index.htm (Abgerufen 07.05.2020).
Mit Backtracking kann man z.B. das Problem des Handlungsreisenden (Hamilton-Kreis), das Finden eines Euler-Zuges, das Kartenfärbeproblem, das Finden einer dominierenden Menge und vieles mehr lösen.
Laufzeitanalyse des Backtracking-Ansatzes
Nachteil des Backtrackings ist seine Laufzeit. Da im schlimmsten Fall alle Möglichkeiten durchprobiert werden müssen, steigt die Laufzeit mit der Anzahl der Knoten/Kanten exponentiell.
Anzahl der Varianten:
n Knoten/Kanten, m Entscheidungsmöglichkeiten => mn Varianten
Das führt z.B. bei der Suche einer dominierenden Menge auf einem Graphen mit 100 Knoten dazu, dass man 2100 = 1,3*1030 Varianten testen muss (es gibt für jeden Knoten zwei Möglichkeiten: Ein Knoten gehört entweder zur dominierenden Menge oder nicht). Das ist selbst mit schnellen Rechnern nicht praktikabel. Bei anderen Problemen ist die Basis oft größer und damit der Zeitaufwand noch höher, da es mehr Möglichkeiten bei jeder einzelnen Entscheidung gibt. In sinnvoller Zeit durchführbar sind daher Algorithmen mit exponentieller Laufzeit nicht. Aber vielleicht gibt es ja bessere Algorithmen...
Hintergrundinformationen: Herunterladen [odt][990 KB]
Weiter zu P=NP?
