Aus­ge­wähl­te Auf­ga­ben aus 9/10

1. Kurze Auf­fri­schung der Grund­la­gen

Ein Zu­falls­ex­pe­ri­ment, das nur zwei Er­geb­nis­se hat, nennt man ein Ber­noul­li-Ex­pe­ri­ment (Z.B. Wer­fen einer Münze W –Z  oder Tref­fer – kein Tref­fer ).

Wird ein Ber­noul­li-Ex­pe­ri­ment  n mal un­ab­hän­gig wie­der­holt, so spricht man von einer Ber­noul­li-Kette der Länge n.

Ist bei einer Ber­noul­li­ket­te p die Wahr­schein­lich­keit für einen Tref­fer, so ist die Wahr­schein­lich­keit für genau k  Tref­fer bei n Wie­der­ho­lun­gen des Ber­noul­li-Ex­pe­ri­ments:

Die Zu­falls­va­ria­ble X heißt dann bi­no­mi­al­ver­teilt mit den Pa­ra­me­tern n und p.

Aus­ge­wähl­te Auf­ga­ben zu 9/10

Auf­ga­be 1
In einem Gefäß U ₁ sind 10 blaue Ku­geln und in einem wei­te­ren Gefäß U ₂ sind 20 rote Ku­geln. Ger­lin­de darf zu­nächst eines der bei­den Ge­fä­ße wäh­len und dar­aus eine Kugel zie­hen. Ist die Kugel rot, dann hat sie einen Preis ge­won­nen.

a) Wie groß ist die Wahr­schein­lich­keit, dass sie einen Preis ge­winnt?

Ger­lin­de hat 50 wei­te­re rote Ku­geln. Sie darf be­stim­men, wie viele davon zu­sätz­lich in U ₁ ge­legt wer­den. Al­ler­dings wer­den dann ge­nau­so viele blaue Ku­geln zu­sätz­lich in U ₂ ge­legt.

b) Ger­lin­de wählt 5 zu­sätz­li­che rote Ku­geln. Hat sich da­durch ihre Ge­winn­wahr­schein­lich­keit ver­bes­sert?

c) Wie viele zu­sätz­li­che rote Ku­geln hätte Ger­lin­de wäh­len müs­sen, um ihre Ge­winn­chan­cen zu ma­xi­mie­ren?

Lö­sung:

Auf­ga­be 2
Eine Klas­se will für einen guten Zweck beim Schul­fest ein Glücks­rad be­trei­ben. Die­ses be­steht aus drei Sek­to­ren mit den fol­gen­den Mit­tel­punkt­swin­keln:
rot: 180°, gelb: 90° und blau: 90°.
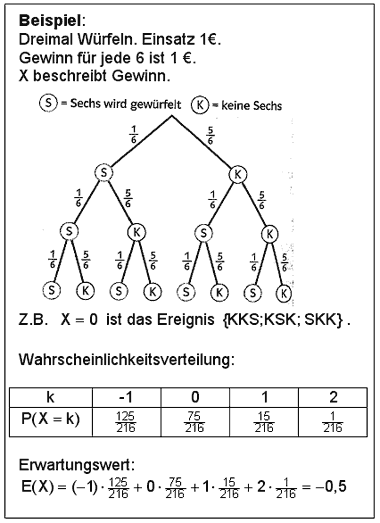
Bei einem Spiel dreht der Kunde das Glücks­rad drei­mal und be­zahlt dafür einen Euro. Er er­hält zwei Euro, wenn er drei­mal die­sel­be Farbe er­reicht, er be­kommt sei­nen Ein­satz zu­rück, wenn genau zwei­mal die­sel­be Farbe an­ge­zeigt wird, in allen an­de­ren Fäl­len wird sein Ein­satz ein­be­hal­ten.

Wel­chen Ge­winn er­zielt die Klas­se mit die­sem Glücks­rad pro Spiel durch­schnitt­lich?

Die Klas­se will im nächs­ten Jahr durch eine Ver­än­de­rung der Sek­to­ren­grö­ßen die Wahr­schein­lich­keit der Fälle, in denen der Ein­satz ein­be­hal­ten wird, er­hö­hen. Dabei sol­len die Spiel­re­geln er­hal­ten blei­ben und der rote Sek­tor soll wei­ter­hin dop­pelt so groß sein wie der gelbe.

Für wel­che Mit­tel­punkt­swin­kel der drei Sek­to­ren ist die Wahr­schein­lich­keit für den Ein­be­halt des Ein­sat­zes am größ­ten?

Lö­sung:

Auf­ga­be 3
Ein Bas­ket­ball­spie­ler hat bei Frei­wür­fen er­fah­rungs­ge­mäß eine Tref­fer­quo­te von 80%, d.h. er trifft durch­schnitt­lich bei 80% sei­ner Würfe.

a) Er wirft 50mal. Die Zu­falls­va­ria­ble X zählt seine Tref­fer. Be­grün­den Sie, dass man X durch eine Bi­no­mi­al­ver­tei­lung mo­del­lie­ren kann. Be­stim­men Sie die Wahr­schein­lich­keit für  35  X  45         

b) Mit wel­cher Wahr­schein­lich­keit trifft der Spie­ler bei drei Frei­wür­fen min­des­tens zwei­mal? Er möch­te gern mit 95% Wahr­schein­lich­keit bei drei Frei­wür­fen min­des­tens zwei­mal
tref­fen. Auf wel­chen Wert muss er dann seine Tref­fer­quo­te ver­bes­sern?

Lö­sung:

Auf­ga­be 4
Ein Com­pu­ter­her­stel­ler be­zieht  von einem Lie­fe­ran­ten Spei­cher­chips.
Er­fah­rungs­ge­mäß sind 80 % der Chips ein­wand­frei.

a) Mit wel­cher Wahr­schein­lich­keit sind von 30 Chips mehr als 20 ein­wand­frei? Die Chips wer­den in Vie­rer­pa­ckun­gen ge­lie­fert. Ab wel­cher An­zahl  Vie­rer­pa­ckun­gen muss mit mehr als 50 % Wahr­schein­lich­keit damit ge­rech­net wer­den, dass in min­des­tens einer Pa­ckung alle Chips de­fekt sind?

b) Wie groß dürf­te die De­fekt­wahr­schein­lich­keit eines Chips höchs­tens sein, damit unter 10 Chips mit min­des­tens 90 % Wahr­schein­lich­keit alle ein­wand­frei sind?

Lö­sung:

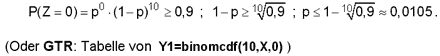
Die ma­xi­ma­le De­fekt­wahr­schein­lich­keit dürf­te höchs­tens etwa 1 % be­tra­gen.