Lösungen zur Wiederholung
Aufträge:
THINK-PAIR-SHARE: LÖSUNGEN auf AB (s.u.)
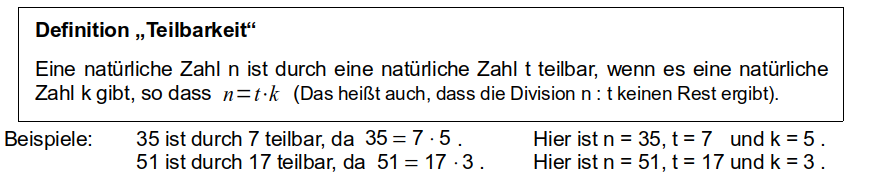
a.) Um die Teilbarkeit einer beliebigen natürlichen Zahl durch die Zahlen 2, 3, 5, 6, 9 und 10 zu untersuchen, hast du bereits Regeln kennen gelernt. Versuche dich zunächst in Stillarbeit an diese Regeln zu erinnern und schreibe alle, die du noch kennst, auf das dafür beigefügte Arbeitsblatt. Nach 5 Minuten darfst du dich leise mit deinem Nachbarn austauschen und ihr könnt eure Regeln gegenseitig korrigieren und ergänzen.
b.) Man unterscheidet „Endstellenregeln“ und „Quersummenregeln“ . Ordne die Regeln aus a.) wenn möglich einer der beiden Kategorien zu und begründe deine Zuordnung.
Begründungsbeispiel: Die Regel „durch 2“ betrachtet nur die letzte Ziffer, die auch als Endstelle bezeichnet wird. Daher ist dies eine Endstellenregel.
-
a.) Untersuche mithilfe der Regeln die folgenden Zahlen auf Teilbarkeit durch die Zahlen
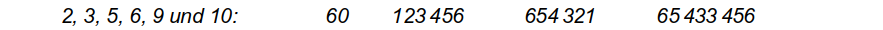
Teiler von 60 sind 2, 3, 5, 6 und 10,
Teiler von 123 456 sind 2, 3, 6
Teiler von 654 321 ist 3
Teiler von 65 433 456 sind 2, 3, 6 und 9
b.) a und b sind frei wählbare Ziffern (von 0 bis 9). Gib jeweils mindestens eine Möglichkeit für die Ziffern a und b so an, dass die Zahl 125 a3b
→ durch 2 teilbar ist:
a kann jede Ziffer sein (also 0 bis 9), b kann jede gerade Ziffer sein, also 0, 2, 4, 6 oder 8.
→ durch 3 teilbar ist:
Die Quersumme ist 11+a+b. Wenn die Summe a+b muss geteilt durch 3 den Rest 1 ergibt, dann ergänzt der Rest 1 die 11 in der Quersumme zur 12. Dadurch ist die gesamte Quersumme durch 3 teilbar. Möglich sind also die Kombinationen (dabei ist beliebig, welche Ziffer jeweils a und welche b ist): 0 und 1, 0 und 4, 0 und 7, 1 und 3, 1 und 6, 1 und 9, 2 und 2, 2 und 5, 2 und 8, 3 und 4, 3 und 7, 4 und 6, 4 und 9, 5 und 5, 5 und 8, 6 und 7, 7 und 9, 8 und 8.
→ durch 6 teilbar ist:
alle Ziffern, die durch 2 und durch 3 teilbare Zahlen ergeben, also nur die Kombinationen aus „durch 3 teilbar“, bei denen b eine / die gerade Zahl der beiden Möglichkeiten ist: 0 und 1, 0 und 4, 0 und 7, 1 und 6, 2 und 2, 2 und 5, 2 und 8, 3 und 4, 4 und 6, 4 und 9, 5 und 8, 6 und 7, 8 und 8.
→ durch 9 teilbar ist:
Die Quersumme ist 11+a+b. Die Summe a+b muss somit geteilt durch 9 den Rest 7 ergeben: 0 und 7, 1 und 6, 2 und 5, 3 und 4, 7 und 9, 8 und 8
→ durch 5 und durch 3 teilbar ist:
alle Ziffern, die durch 3 teilbare Zahlen mit der Endziffer 5 oder 0 ergeben. Es muss also b=5 oder b=0 sein. Verbleiben die Kombinationen für a und b: 1 und 0; 4 und 0; 7 und 0; 5 und 2; 5 und 5; 8 und 5.
-
Die Zahlen a, b und t seien natürliche Zahlen. Formuliere zunächst ein paar konkrete Zahlenbeispiele für die folgenden Sätze zur Teilbarkeit. Begründe die Sätze dann mithilfe der (oben stehenden) Definition.
Es liegen Hilfekärtchen bereit, wenn du nicht weiterkommst.

zu 1a.)
z.B. 12 + 16: 12 ist durch 4 teilbar, 16 auch, 12 + 16 = 28 ebenfalls.
a ist durch t teilbar, also a = k · t
b ist durch t teilbar, also b = g · t
Somit ist a + b = k · t + g · t = (k + g) · t
Da k + g eine natürliche Zahl ist, ist die Definition „Teilbar durch t“ für die Summe a + b erfüllt.
zu 1b.)
z.B. 12 ist durch 4 teilbar, 7 nicht, 12 + 7 = 19 ist nicht durch 4 teilbar.
a ist durch t teilbar, also a = k · t
b ist nicht durch t teilbar, also b = g · t + x, wobei 0 < x < t (x ist der Rest).
a + b = k · t + g · t + x = (k + g) · t + x , bei Division mit t ergibt sich der Rest 0 < x < t, also ist a + b nicht durch t teilbar.
zu 2.)
z.B. 12 ist durch 4 teilbar, 7 nicht, 12 · 7 = 84 ist durch 4 teilbar.
a ist durch t teilbar, also a = k · t
b ist eine beliebige natürliche Zahl.
a + b = k · t · b = (k · b) · t . Da k · b eine natürliche Zahl ist, ist die Teilbarkeitsdefinition „durch t“ für das Produkt erfüllt.
-
a.) Überprüfe ohne Taschenrechner, ob die folgenden Summen jeweils durch 3 teilbar sind. Benenne und erkläre: In welchen Fällen nützt dir Satz 1 aus 3a.) etwas, wann nicht?
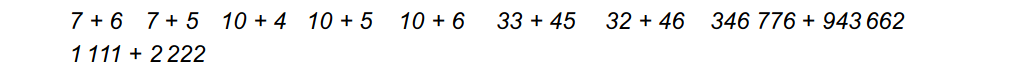
Satz 1 kann dann nichts aussagen, wenn beide Summanden nicht durch 3 teilbar sind, also bei 7 + 5, 10 + 4, 10 + 5, 32 + 46 und 1 111 + 2 222.
Durch 3 teilbar sind: 7 + 5, 10 + 5, 33 + 45, 32 + 46, 346 776 + 943 662 und 1 111 + 2 222,
die anderen entsprechend nicht.
b.) Überprüfe, ob die folgenden Produkte jeweils durch 9 teilbar sind. Benenne und erkläre: In welchen Fällen nützt dir Satz 2 aus 3a.) etwas, wann nicht?
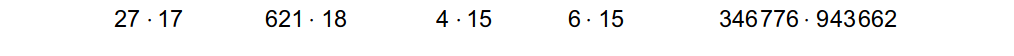
Satz 2 nützt immer dann, wenn mindestens ein Faktor durch 9 teilbar ist, also bei 27 · 17 und 621 · 18.
Sobald beide Faktoren nicht durch 9 teilbar sind, kann das Produkt nur danndurch 9 teilbar sein , wenn beide Faktoren jeweils durch 3 teilbar sind, wie bei 6 · 15 und bei 346776 · 943662. Ansonsten nicht, wie bei 4 · 15. Dies wird aber durch Satz 2 nicht abgedeckt.
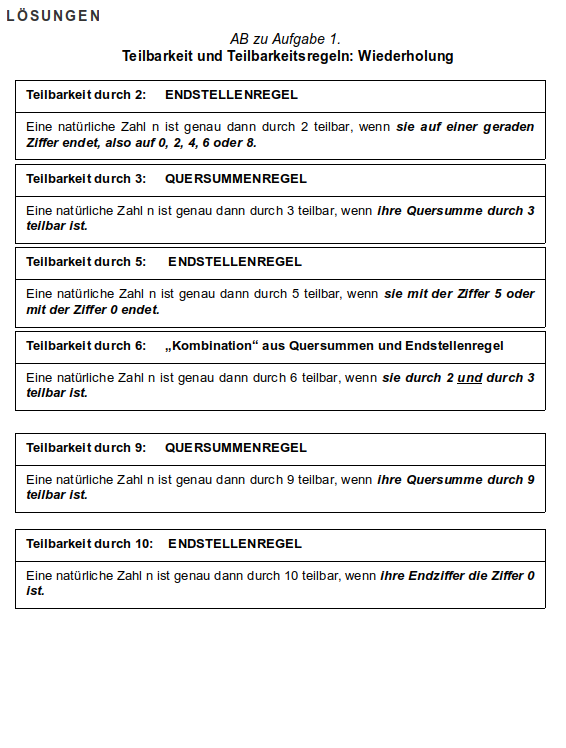
AB Lösungen zu Aufgabe 1
AB Lösungen zu Aufgabe 1, Seite 2 von 11
Teilbarkeit und Teilbarkeitsregeln – Lösungen: Herunterladen [odt][394 KB]
Teilbarkeit und Teilbarkeitsregeln – Lösungen: Herunterladen [pdf][237 KB]
Weiter zu Weitere Regeln
