Der Eu­kli­di­sche Al­go­rith­mus – Lö­sun­gen

Ent­de­cker-Auf­trä­ge:

1. Be­trach­te die Zah­len 56 und 32. Es gilt ggT(32; 56) = 8. Wir zer­le­gen nun beide Aus­gangs­zah­len mit­hil­fe ihres ggT und er­hal­ten 32 = 4 · 8 und 56 = 7 · 8. Mit­hil­fe die­ser Zer­le­gun­gen kann man über die Dif­fe­renz 56 – 32 aus­sa­gen, dass sie 3 · 8 sein muss, ohne sie ex­pli­zit aus­zu­rech­nen.

   a.) Be­grün­de diese Aus­sa­ge.

   56 − 32 = 7 · 8 − 4 · 8 = (7 − 4) · 8 = 3 · 8

   

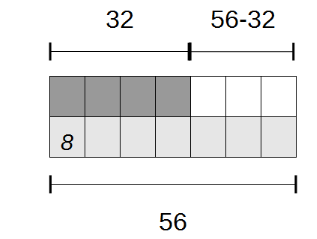
   Oder an­schau­lich mit ne­ben­ste­hen­der Ab­bil­dung: Die 8 wird als Maß­zahl ver­wen­det. Laut Vor­ga­be passt sie vier­mal in die 32 (dun­kel­grau) und sie­ben­mal in die 56 (hell­grau). Somit passt die 8 also drei­mal in die Dif­fe­renz von 56 und 32 (weiß).

   b.) Aus die­sem Wis­sen folgt eine wei­te­re Aus­sa­ge: Die Dif­fe­renz 56 – 32 ist eben­falls durch 8 teil­bar, d.h. der ggT von 56 und 32 teilt auch die Dif­fe­renz 56 – 32. Be­grün­de.

   Der ggT ist Tei­ler von bei­den „Sum­man­den“ (Mi­nu­end und Sub­tra­hend), also kann er aus­ge­klam­mert wer­den. Somit lässt sich die Dif­fe­renz als „Klam­mer mal 8 (=ggT)“ schrei­ben, wobei in der Klam­mer eine na­tür­li­che Zahl steht. Dies ent­spricht aber der De­fi­ni­ti­on für die Teil­bar­keit durch 8 (also den ggT), die Dif­fe­renz ist also durch 8 (den ggT) teil­bar.

   c.) Die­ses Vor­ge­hen funk­tio­niert nicht nur für die Zah­len 56 und 32, son­dern für be­lie­bi­ge Zah­len. Führe es an den Zah­len­paa­ren 25 und 35, 4 und 12 sowie 26 und 65 er­neut durch.

   35 − 25 = 7 · 5 − 5 · 5 = (7 − 5) · 5 = 2 · 5

   12 − 4 = 3 · 4 − 1 · 4 = (3 − 1) · 4 = 2 · 4

   65 − 26 = 5 · 13 − 2 · 13 = (5 − 2) · 13 = 3 · 13

2. Dar­über hin­aus kann man zei­gen, dass der ggT von 56 und 32 nicht nur „ir­gend­ein“ Tei­ler von 56 – 32 ist, son­dern dass er sogar der ggT von 56 – 32 und 32 sein muss.

   a.)* Be­grün­de diese Aus­sa­ge.

   Wir wis­sen: Der ggT von 56 und 32 teilt 56 – 32.

   Soll­te dies nicht der ggT von 56 – 32 und 32 sein, so müss­te es einen grö­ße­ren Tei­ler von 56 – 32 und 32 geben, als den ggT von 56 und 32. Da die­ser Tei­ler in der Dif­fe­renz 56 – 32 den Mi­nu­en­den 32 teilt, muss er auch Tei­ler von 56 sein (nach dem ent­spre­chen­den Satz über die Teil­bar­keit von Sum­men). Somit wäre er auch ge­mein­sa­mer Tei­ler von 56 und 32, der grö­ßer wäre als deren ggT – das ist nicht mög­lich (weil er sonst der ggT wäre).

   Also muss der ggT von 56 und 32 auch der ggT von 56 – 32 und 32 sein.

   b.) Diese Er­kennt­nis hat der grie­chi­sche Ma­the­ma­ti­ker Eu­klid von Alex­an­dria 325 v. Chr. In sei­nem Werk „Die Ele­men­te“ wei­ter­ge­führt. Er ent­wi­ckel­te dar­aus den so­ge­nann­ten Eu­kli­di­schen Al­go­rith­mus, mit dem man den ggT zwei­er Zah­len be­stim­men kann. Am Bei­spiel der Zah­len 56 und 32 geht der Al­go­rith­mus so:

   ggT(56; 32) = ggT(24; 32) = ggT(24; 8) = ggT(16; 8) = ggT(8; 8) = 8

   Über­le­ge dir, wie Eu­klid von links nach rechts in die­ser „Ket­ten­glei­chung“ vor­geht. Über­prü­fe dein Vor­ge­hen an den Zah­len­paa­ren aus 1c.), indem du deren ggT mit dem glei­chen Vor­ge­hen be­stimmst und mit den ggT-Wer­ten aus dei­nen Lö­sun­gen von 1c.) ab­gleichst. Schrei­be dann eine An­lei­tung, wie man auf diese Weise den ggT zwei­er be­lie­bi­ger Zah­len be­stim­men kann. Es lie­gen Hil­fe­kärt­chen be­reit, falls du nicht wei­ter­kommst.

   Eu­klid er­setzt immer die grö­ße­re der bei­den Zah­len durch die Dif­fe­renz aus der grö­ße­ren und der klei­ne­ren Zahl. Nach a.) ver­än­dert sich da­durch der ggT nicht. Am Schluss ver­bleibt ein ggT mit zwei glei­chen Zah­len – dies ist der ggT der bei­den Aus­gangs­zah­len.

   Bei­spie­le:

   ggT(35;25) = ggT(10;25) = ggT(10;15) = ggT(10;5) = ggT(5;5) = 5

   ggT(12;4) = ggT(8;4) = ggT(4;4) = 4

   ggT(65;26) = ggT(39;26) = ggT(13;26) = ggT(13;13) = 13

3. Führe den Eu­kli­di­schen Al­go­rith­mus an den fol­gen­den Zah­len­paa­ren durch.

   a.) 9 und 30

   ggT(9;30) = ggT(9;21) = ggT(9;12) = ggT(9;3) = ggT(6;3) = ggT(3;3) = 3

   b.) 226 und 904

   ggT(226;904 = ggT(226;678) = ggT(226;452) = ggT(226;226) = 226

   c.) 1215 und 2115

   ggT(1215;2115) = ggT(1215;900) = ggT(315;900)

   = ggT(315;585) = ggT(315;270) = ggT(45;270) = ggT(45;225)

   = ggT(45;180) = ggT(45;135) = ggT(45;90) = ggT(45;45) = 45

4. * Pro­gram­mie­re den Eu­kli­di­schen Al­go­rith­mus so, dass der An­wen­der zwei Zah­len ein­ge­ben kann und den ggT als Aus­ga­be er­hält.

   Lö­sungs­da­tei in Scratch: Eu­kli­di­scher­Al­go­rith­mus.sb2 (Autor: Tom Schal­ler)

   Lö­sungs­da­tei im Ap­pIn­ven­tor: gg­t_­eu­klid.apk im Ord­ner 7_apps (Au­to­rin: Mo­ni­ka Ei­sen­mann)

Der Eu­kli­di­sche Al­go­rith­mus – Lö­sun­gen: Her­un­ter­la­den [odt][112 KB]

Der Eu­kli­di­sche Al­go­rith­mus – Lö­sun­gen: Her­un­ter­la­den [pdf][116 KB]

Wei­ter zu APPs