Winkelweiten – Lösungen

1. Sternfünfeck und Sternsiebeneck

   a) Seien α, β und γ die Innenwinkel im Dreieck AFG. Für ihre Nebenwinkel gilt dann ∠CGE=180°-α bzw. ∠BFD=180°-β (Außenwinkelsatz für Dreieck AFG). Im Dreieck GCE sind die beiden rot gefärbten Innenwinkel des Sternfünfecks zusammen so groß wie α+β (Winkelsumme). Ebenso sind die beiden blau gefärbten Innenwinkel im Dreieck FBD zusammen so groß wie β. Insgesamt folgt für die Innenwinkelsumme des Sternfünfecks α+β+γ, sie entspricht also der Winkelsumme eines Dreiecks.

   

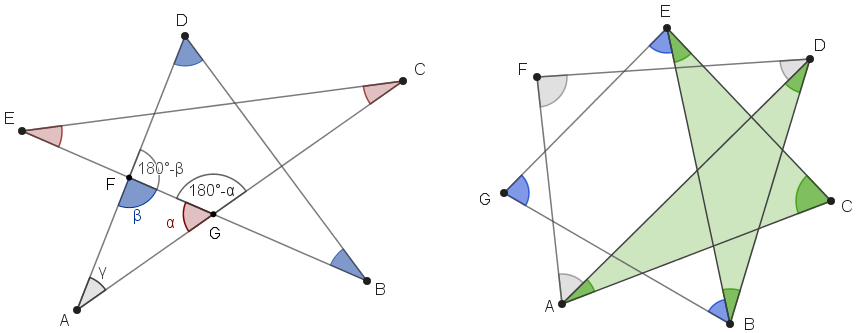
   b) Die Winkelsumme des Sternsiebenecks kann man auf die des Sternfünfecks zurückführen. Man zeichnet z.B. das Sternfünfeck ABCDE ein (hier grün gefärbt) und erkennt, dass zu dessen Winkelsumme von 180° noch die Winkelsummen der Dreiecke ADF und BEG hinzukommen, bis alle Innenwinkel des Sternsiebenecks berücksichtigt sind.

   Ein Sternsiebeneck besitzt daher die Winkelsumme 3 · 180° = 540°.

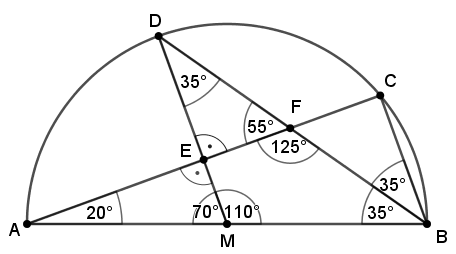
2. a) Nach Voraussetzung sind die Dreiecke ABC, BCF, EFD und AME rechtwinklig, das Dreieck BDM ist gleichschenklig mit der Basis BD. Mit Scheitel- und Nebenwinkeln sowie der der Winkelsumme im Dreieck berechnet man schrittweise die eingetragenen Winkel.

   
   

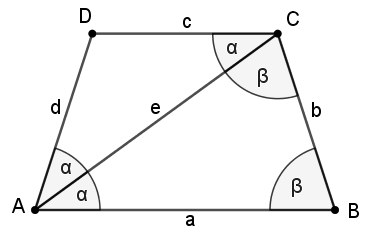
   b) Die geforderte Zerlegung ist nur möglich, wenn im Trapez c=d und a=e gilt.

   Aus den Winkeleigenschaften gleichschenkliger Trapeze und Dreiecke folgen die oben eingetragenen Winkelbeziehungen. Es gilt weiterhin:

   (1) β=2α (Basiswinkel im Trapez)

   (2) α=180°-2β (Winkelsumme im Dreieck ABC).

   Setzt man (1) in (2) ein, so folgt α = 180°-2·(2α) ⇔ 5α=180°, also α=36°.

   Die Innenwinkel des Trapezes sind damit β=72° und α+β=108° weit.

3. a) Bezeichnungen siehe Skizze unten links.

   α = 34° (Wechselwinkel an parallelen Geraden)

   β = 180°‒ 2·34° = 112° (Winkelsumme im gleichschenkligen Dreieck ABM)

   δ = α + β = 112°+34°=146° (δ = ∠AMC, Innenwinkel bei Punkt M)

   ε = (180°‒ 146°) : 2 = 17° (Winkelsumme im gleichschenkligen Dreieck ACM)

   φ = 180°‒ (112°+17°) = 51° (Winkelsumme im Dreieck ADM)

   Skizze zu a)

   

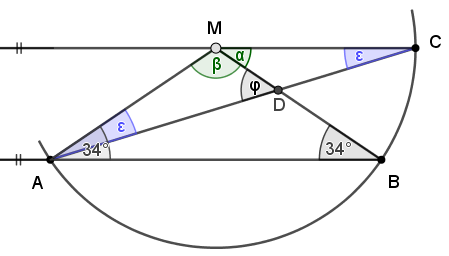
   Skizze zu b)

   

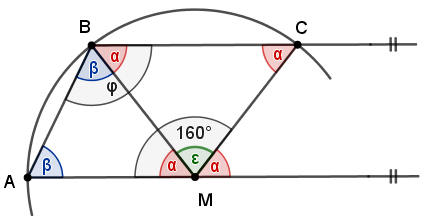
   b) Bezeichnungen siehe Skizze oben rechts.

   α = 20° (Nebenwinkel am Punkt M, Wechselwinkel an MC)

   α = 20° (Basiswinkel im gleichschenkligen Dreieck MCB)

   [ε = 180° ‒ 2·20° = 140°] (Winkelsumme im gleichschenkligen Dreieck MCB)]

   α = 20° (Wechselwinkel an Strecke BM)

   β = 180°‒ 20°) : 2 = 80° (Winkelsumme im gleichschenkligen Dreieck AMB)

   φ = 80° + 20° = 100°

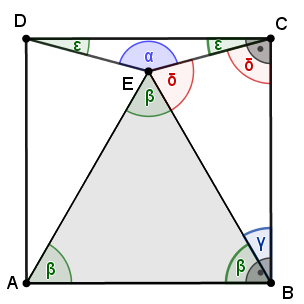
4. β = 60° (Winkelsumme im gleichseitigen Dreieck)

   γ = 90°- 60° = 30° (rechter Winkel im Quadrat bei B)

   δ = (180°‒ 30°) : 2 = 75° (Winkelsumme im gleichschenkligen Dreieck BCE)

   ε = 90° - 75° = 15° ( rechter Winkel im Quadrat bei C)

   α = 180°‒ 2·15° = 150° (Winkelsumme im gleichschenkligen Dreieck ECD)

Hinweis zu Aufgaben 1,3 und 4:

Zur Visualisierung der Zusammenhänge und Reflexion können die Schritte in den GeoGebra-Applets nacheinander eingeblendet werden:

zu 1) 01_geo_ab_Nr1_Sternvielecke.ggb

zu 3a ) 01_geo_ab_Nr3a_Winkel_am Kreis.ggb

zu 3b ) 01_geo_ab_Nr3b_Winkel_am Kreis.ggb

zu 4 ) 01_geo_ab_Nr4_Winkel_im Quadrat.ggb

Nr. 2 ist als reine Übungsaufgabe gedacht.

 

Winkelweiten – Lösungen: Herunterladen [odt][417 KB]

Winkelweiten – Lösungen: Herunterladen [pdf][247 KB]

 

Weiter zu Entdecken und Beweisen