Graphen
„Ein Graph […] ist in der Graphentheorie eine abstrakte Struktur, die eine Menge von Objekten zusammen mit den zwischen diesen Objekten bestehenden Verbindungen repräsentiert. Die mathematischen Abstraktionen der Objekte werden dabei Knoten (auch Ecken) des Graphen genannt. Die paarweisen Verbindungen zwischen Knoten heißen Kanten (manchmal auch Bögen1). […] Häufig werden Graphen anschaulich gezeichnet, indem die Knoten durch Punkte und die Kanten durch Linien dargestellt werden.“2
Man unterscheidet ungerichtete von gerichteten Graphen, bei denen Kanten nur in ausgewiesenen Richtungen durchlaufen werden dürfen. Außerdem wird zwischen Graphen mit Mehrfachkanten und Graphen ohne Mehrfachkanten unterschieden:
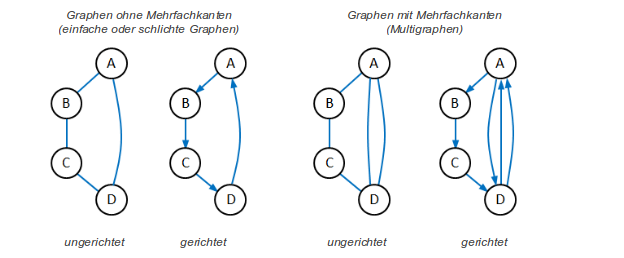
Bildquellen: Graph ungerichtet [CC0] via Wikimedia Commons; Graph gerichtet [CC0] via Wikimedia Commons; Graph ungerichtet Mehrfachkanten [CC0] via Wikimedia Commons; Graph gerichtet Mehrfachkanten [CC0] via Wikimedia Commons , Autor: Tobias Knerr;
„Den Zusatz „ohne Mehrfachkanten“ lässt man gewöhnlich weg und nennt Graphen mit Mehrfachkanten Multigraphen. Ferner verzichtet man meist auf das Attribut „ungerichtet“ und kennzeichnet nur gerichtete Graphen explizit. Ungerichtete Graphen ohne Mehrfachkanten nennt man auch häufig schlicht oder einfach. Eine andere Bezeichnung für gerichtete Graphen ist Digraph (Directed Graph)“3
Bei der Einführung beschäftigen wir uns nur mit ungerichteten Graphen, erste Beispiele:
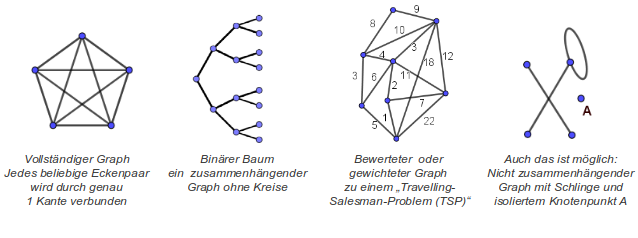
1 Bögen werden bisweilen auch als gerichtete Kanten aufgefasst.
2 Wikipedia: siehe Seite „Graph ( Graphentheorie)“, URL: https://de.wikipedia.org/wiki/Graph_(Graphentheorie) (abgerufen: 28.03.2018)
3 a.a.O.
Einführung von Fachbegriffen
Im vorliegenden Material werden die Begriffe Ecke, Knoten und Knotenpunkt synonym verwendet, wobei die Verwendung des im Bildungsplan gewählten Begriffs Knotenpunkt statt Ecke bevorzugt wird.
Graphen werden als topologische Strukturen auf Basis mengentheoretischer Begriffe definiert:
Definition:
Ein Graph G ist ein geordnetes Paar ( V , E ) , wobei V eine Menge von Knoten (englisch vertex / vertices, oft auch Ecken genannt) und E eine Menge von Kanten (engl. edge / edges, manchmal auch Bögen genannt) bezeichnet.4
Für die Einführung in Klasse 8 bieten sich dagegen nur didaktisch reduzierte Definitionen an, die einen anschaulichen Zugang ermöglichen, z.B.:
Ein Graph ist eine geometrische Figur aus endlich vielen Knotenpunkten und Kanten, die einige dieser Punkte verbinden. Die Kanten müssen nicht geradlinig verlaufen und können sich überkreuzen. Mehrfachkanten, Schlingen und isolierte Knoten sind ebenfalls zugelassen.
oder auch knapper:
Ein Graph ist ein Gebilde, das aus Knotenpunkten5 und Kanten besteht. Jede Kante verbindet 2 Knotenpunkte.
Im letzten Kasten ist zunächst auch alles gesagt. Was nicht explizit genannt wird, muss entdeckt werden. Da es im Unterricht vor allem auf die Präzisierung dessen ankommt, was nicht notiert wurde, sollte erarbeitet werden, dass Mehrfachkanten, Schlingen oder isolierte Ecken erlaubt sind.
4 Wikipedia: siehe Seite „Graph ( Graphentheorie)“, URL: https://de.wikipedia.org/wiki/Graph_(Graphentheorie) (abgerufen: 28.03.2018). Die Kantenmenge E wird im Falle einfacher Graphen und Multigraphen auch als Menge aller zweielementigen Teilmengen der Menge V betrachtet, da eine Kante durch die beiden Knoten an ihren Enden eindeutig festgelegt werden kann.
5 Der im Bildungsplan verwendete Begriff Knotenpunkt kann hilfreich sein, wenn man die Visualisierung als Punkt betonen möchte, ansonsten ist die Bezeichnung Knoten üblich. Im Unterricht bietet sich auch ein Rückgriff auf die Bezeichnung „Verkehrsknotenpunkt“ in Straßen- oder Bahnnetzen an.
Unterschiedlich verwendete Begriffe
In der Graphentheorie bezeichnen die Begriffe Weg, Pfad, Kantenzug oder Kantenfolge eine Folge von Knoten, in welcher jeweils zwei aufeinander folgende Knoten durch eine Kante verbunden sind. Leider werden diese und weitere Begriffe aber nicht einheitlich verwendet. Bei einem Kantenzug dürfen Knoten und Kanten mehrmals durchlaufen werden, bei einem Weg darf dagegen jeder Knoten nur einmal enthalten sein. Da es hier um einige elementare Bedeutungsunterschiede geht, muss im Unterricht besonders darauf geachtet werden, eine in sich stimmige Terminologie zu verwenden.
Daher wurde im letzten Abschnitt dieses Kapitels eine Begriffsübersicht eingebunden, damit Sie dort bei Bedarf auch gezielt nachschlagen können. Die getroffene Auswahl deckt dabei den Großteil der für die Einführung relevanten Begriffe ab. Eine ausführlichere Übersicht hat Manfred Nitzsche in seinem empfehlenswerten Buch „Graphen für Einsteiger“ in Form eines „Kleinen Wörterbuches der Graphentheorie“ zusammengestellt.6
6 Vgl. „Kleines Wörterbuch der Graphentheorie“, in Nitzsche: „Graphen für Einsteiger“, Vieweg+Teubner, Wiesbaden, 2009, 3. Auflage
Isomorphe Graphen (Ausflug in die Topologie)
Ein Graph bezeichnet eine Struktur und ist ein topologischer Begriff, da es auf die Länge der Kanten oder die Winkel zwischen den Kanten nicht ankommt.7
Das bekannte „Haus des Nikolaus“ kann gut als Ausgangspunkt dienen, um zu veranschaulichen, dass man beim Zeichnen eines Graphen viele Freiheiten hat8: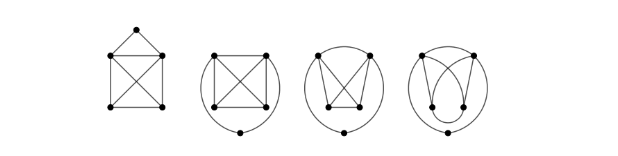
Das Haus des Nikolaus wird schrittweise zu topologisch äquivalenten Graphen „verformt.“
Diese Repräsentationen von Graphen lassen sich durch elastische Verformungen ineinander überführen, sie sind topologisch äquivalent. Die gemeinsamen Eigenschaften (Beziehungen zwischen Knoten und Kanten) lassen sich dabei übersichtlich in einer Tabelle bzw. Matrix darstellen, die dann jeweils eine Klasse topologisch äquivalenter Graphen repräsentiert.
7 Eintrag Graph, in: „Schülerduden Die Mathematik I“, Dudenverlag, 1990, 5. Auflage, S.162
8 vgl. Nitzsche: „Graphen für Einsteiger“, Vieweg+Teubner, Wiesbaden, 2009, 3. Auflage, S.5
Graph als Tabelle – Adjazenz- und Inzidenzmatrizen
In die Adjazenzmatrix (bzw. Nachbarschaftsmatrix) eines Graphen wird an jeder Stelle die Anzahl der Kanten eingetragen, die zwischen den Knotenpaaren existieren. Bei n Knoten erhält man eine quadratische n x n -Matrix. In der Praxis werden auch häufig Adjazenzlisten zu den einzelnen Knoten angelegt, in denen jeweils alle benachbarten Knoten aufgelistet werden.
In der Inzidenzmatrix (Knoten-Kanten-Matrix) steht eine „1“, wenn ein Knoten auf einer Kante liegt, andernfalls eine „0“. Bei n Knoten und m Kanten ergibt sich so eine n x m – Matrix.
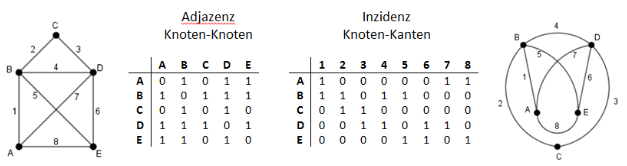
Abb: Adjazenz- und Inzidenztabelle zum Haus des Nikolaus und topologisch äquivalenten Graphen9
9Die Verformung kann mit der Datei 04_aug_animierte_Umformung_Haus_des_Nikolaus.ggb animiert werden, mit der Datei 04_aug_Umformung_Haus_des_Nikolaus.ggb können die Stadien der Verformung schrittweisen visualisiert und erläutert werden.
Exkurs zu Datenstrukturen:
„Für die Repräsentation von Graphen im Computer gibt es im Wesentlichen zwei gebräuchliche Formen: die Adjazenzmatrix [...] und die Adjazenzliste (Nachbarschaftsliste). Die Bedeutung der beiden Darstellungen liegt darin, dass praktisch jede algorithmische Lösung graphentheoretischer Probleme auf wenigstens eine der beiden Repräsentationen zurückgreift. Eine weitere, aber seltener genutzte Möglichkeit zur Darstellung von Graphen im Computer ist die Inzidenzmatrix [...]. Inzidenzmatrizen sind zwar aufwändiger zu implementieren und zu verwalten, bieten aber eine Reihe von Vorteilen gegenüber Adjazenzmatrizen. Zum einen verbrauchen sie bei fester Anzahl von Kanten stets nur linear viel Speicherplatz bezüglich der Anzahl der Knoten, was insbesondere bei dünnen Graphen (also Graphen mit wenig Kanten) von Vorteil ist, während die Adjazenzmatrix quadratischen Platzbedarf bezüglich der Anzahl der Knoten besitzt (dafür aber kompakter bei dichten Graphen, also Graphen mit vielen Kanten ist). Zum anderen lassen sich viele graphentheoretische Probleme nur mit Adjazenzlisten in linearer Zeit lösen. In der Praxis verwendet man daher meist diese Form der Repräsentation.“10
10Wikipedia, siehe Seite „Graph (Graphentheorie)“, URL: https://de.wikipedia.org/wiki/Graph_(Graphentheorie)#Definitionen (abgerufen: 30.3.2018)
Mögliche Berücksichtigung im Unterricht
Die Behandlung von Matrizen bzw. Tabellen ist im Rahmen dieser Einheit nicht explizit vorgesehen. Gleichwohl handelt es sich um einen wichtigen Aspekt, der gerade in Hinblick auf die Vernetzung mit den Inhalten des Moduls Informatik angesprochen bzw. im Rahmen binnendifferenzierender Phasen eingebracht werden sollte. Hierzu ein Beispiel11:
Aus einer einfach gehaltenen Adjazenzmatrix sollen die Schülerinnen und Schüler mögliche Graphen skizzieren und vergleichen.
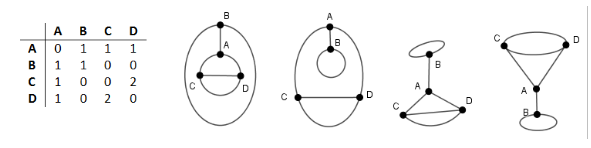
Die Umkehrung der Aufgabenstellung liefert aus didaktischer Sicht den schönen Nebeneffekt, dass die topologische Äquivalenz von Graphen und die zentrale Bedeutung der Matrizen (bzw. in Klasse 8 Tabellen) während der Bearbeitung intuitiv erfasst werden können.
Durch den Darstellungswechsel zwischen Bild und Tabelle wird außerdem ein deutlich tieferes Verständnis der bereits eingeführten Begriffe erreicht. Ein mögliches Umsetzungsbeispiel wurde daher für die 4. Stunde der Einheit ausgewiesen.
11vgl. Abb.7 des Eintrags „Verformungen“, in „Schülerduden: Die Mathematik I“, Dudenverlag, 1990, 5. Auflage, S.474 Hinweis: Die Adjazenzmatrix in Abb. 7 wird hier fälschlicherweise als „Inzidenzmatrix“ bezeichnet.
Auswahl der Problemstellungen für den Unterricht
Das Nachzeichnen eines Graphen in einem Zug unter den Bedingungen, dass
- keine Kante doppelt durchlaufen wird
- alle Kanten durchlaufen werden und
- Start- und Zielecke identisch sind
führt zunächst zu geschlossenen eulerschen Kantenzügen (Eulertouren) bzw. den sog. Eulergraphen. Lässt man die Bedingung (3) weg, so erhält man offene Eulersche Kantenzüge. Mit notwendigen und hinreichenden Bedingungen für die Existenz Eulerscher Kantenzüge lässt sich dann das bekannte Königsberger Brückenproblem lösen. Ähnliche Probleme (Wohnungsrundgang, Nachtwächterproblem,…) wurden ergänzend aufgenommen, um den Umgang mit Eulergraphen zu vertiefen.
Die Suche nach einem Weg durch alle Knoten eines Graphen führt danach zu Hamilton-Kreisen bzw. Hamiltongraphen, wobei hier nicht zwingend alle Kanten durchlaufen werden müssen. Einfache „Travelling-Salesman-Probleme“ bieten sich danach an, um bewertete Graphen einzuführen und erste anwendungsorientierte Aspekte in den Blick zu nehmen. So kann man am Beispiel der Suche nach dem „kürzesten“ Hamiltonkreis auch den Bogen zu ungelösten Problemen der Graphentheorie schlagen. Für einen gegebenen Graphen kann man zwar wie im Unterricht theoretisch überprüfen, ob Hamiltonkreise existieren und deren „Länge“ anschließend vergleichen, dieses Vorgehen ist aber für für größere Graphen praktisch nicht ausführbar, da zu viele Daten anfallen würden. „Leider gibt es […] auch kein bekanntes notwendiges und hinreichendes Kriterium für die Existenz von Hamilton-Kreisen, das wesentlich schneller ausführbar wäre. Tatsächlich gehört die Frage nach der Existenz von Hamiltonkreisen in Graphen zu den algorithmisch schwierigsten Problemen der Matehmatik, die auch NP-vollständige Probleme genannt werden.“12
Als weitere Anwendung bieten sich Sitzordnungsprobleme an, deren Beziehungsgefüge als Hamiltonsche Graphen betrachtet werden können. Jede mögliche Sitzordnung entspricht einem Hamilton-Kreis des Graphen, so dass die Suche nach Hamilton-Kreisen direkt als Teil einer Lösungsstrategie für diese Art von Logikrätseln motiviert werden kann. Im Unterrichtsgang wird dieser Zusammenhang in der 5. Stunde behandelt, da er sich besonders gut zur Vernetzung von Graphentheorie und Aussagenlogik eignet und so eine überzeugende Verzahnung dieser Gebiete erreicht werden kann.
Für praktische Probleme sind gerichtete Graphen sehr bedeutsam, deren Behandlung im Lehrplan in Klasse 8 nicht vorgesehen ist. Um sie auf einer intuitiven Basis einzubinden, wurden im Bereich der Logikrätsel Überfahrt- und Umfüllprobleme ausgewählt, für die übersichtliche Lösungsstrategien auf der Betrachtung von Kantenzügen in gerichteten Graphen beruhen.
Die in Klasse 9 im Bereich der Informatik vorgesehene Behandlung des Algorithmus von Dijkstra zur Wegsuche in einem Graphen (vgl. BP 3.2.1.1 (6) ) baut auf diesen Zusammenhängen auf.
12Tittman, Peter: „Graphentheorie“, Hanser-Verlag, 2011, 2. Auflage, S. 122, ergänzend hierzu aus dem Wikipedia-Artikel zur NP-Vollständigkeit [https://de.wikipedia.org/wiki/NP-Vollständigkeit (abgerufen am 25.4.18)]: „In der Informatik bezeichnet man ein Problem als NP-vollständig (vollständig für die Klasse der Probleme, die sich nichtdeterministisch in Polynomialzeit lösen lassen), wenn es zu den schwierigsten Problemen in der Klasse NP gehört [...]. Dies bedeutet umgangssprachlich, dass es sich vermutlich nicht effizient lösen lässt“. Hintergrundinformationen zu den Komplexitätsklassen P und NP findet man z.B. in Aigner, Martin.: „Diskrete Mathematik“, Vieweg-Verlag, 2006, 6. Auflage, Kap. 8.5, S. 161f.
Hintergrundinformationen: Herunterladen [odt][526 KB]
Hintergrundinformationen: Herunterladen [pdf][451 KB]
Weiter zu Aussagenlogik
