Weitere Endstellen- und Quersummenregeln

Aufträge in Stillarbeit:

Begründe die 5er-Regel.
Es liegen Hilfekärtchen bereit, wenn du nicht weiterkommst.

Jede Zahl lässt sich zerlegen in eine Summe aus ihren „Einern“ und dem Rest, z.B. 123 = 3 + 120. Der Rest ist auf jeden Fall ein Vielfaches von 10 und somit durch 5 teilbar. Somit folgt aus Satz 1, dass die Zahl nur dann durch 5 teilbar ist, wenn die „Einer“ es sind, also nur bei den „Einern“ 0 oder 5. Die „Einer“ entsprechen aber der letzten Ziffer der Zahl, wodurch die Endstellenregel begründet ist.
Formuliere die Endstellenregel zur Teilbarkeit durch 100 und begründe sie.

Die Teilbarkeitsregel durch 100 ist eine Endstellenregel über die beiden letzten Stellen: Eine Zahl ist genau dann durch 100 teilbar, wenn ihre letzten beiden Ziffern beide 0 sind. Die Begründung verläuft wie die Begründung der 5er-Regel, man trennt aber in eine Summe aus einer Zahl, die aus den letzten beiden Ziffern entsteht (also zwischen 0 und 99 liegt) und einer Zahl, die nur ganzzahlig viele 100er beinhaltet. Letztere ist durch 100 teilbar, somit ist die Summe nur bei der ersten Zahl 0 (die aus den Ziffern 00 entsteht) durch 100 teilbar.
Auch die Teilbarkeit durch 4 lässt sich mithilfe einer Endstellenregel, die auf den letzten beiden Ziffern beruht, prüfen. Formuliere und begründe sie.

Eine Zahl ist durch 4 teilbar, wenn die aus ihren letzten beiden Ziffern gebildete Zahl durch 4 teilbar ist.

Begründung: Auch hier trennt man in die letzten beiden Ziffern und eine „Hunderterzahl“. Da die „Hunderterzahl“ durch 4 teilbar ist, ist die Summe durch 4 teilbar, wenn die Zahl, die aus den letzten beiden Ziffern entsteht, durch 4 teilbar ist.
Finde die Regel zur Teilbarkeit durch 8, formuliere und *begründe sie.

Eine Zahl ist durch 8 teilbar, wenn die aus ihren letzten drei Ziffern gebildete Zahl durch 8 teilbar ist.

Begründung: Da 8 nicht jeder „Zehnerzahl“ und nicht jeder „Hunderterzahl“ teilt, reichen zwei Stellen nicht aus. 8 teilt aber jeder „Tausenderzahl“! Deshalb bildet man auch hier wieder eine Summe aus der Zahl, die aus den letzten drei Ziffern gebildet wird, und dem Rest, der dann eine aus ganzzahligen 1000ern bestehende Zahl ist. Letztere ist durch 8 teilbar, also ist die Summe durch 8 teilbar, wenn es die Zahl aus den letzten drei Ziffern ist.

Beispiel: 53 248 = 53 000 + 248. In die 53 000 passt die 8, da dies eine „Tausenderzahl“ ist. Nun muss noch die 248 geprüft werden. Da 248 : 8 = 36 ist auch die 53 248 durch 8 teilbar.

Quersummenregeln

Die Begründung für die Teilbarkeiten mit Quersummenregeln lassen sich am besten an Beispielen durchführen. Wichtig dabei ist es, dass die Vorgehensweise allgemeingültig ist, d.h. an jeder Zahl möglich wäre, also nicht nur am gewählten Beispiel.

Ihr erhaltet eine Begründung für die 9er-Regel.

a.) Lest die Regel durch und besprecht sie so, dass ihr jeden Schritt erklären könnt.

b.) Begründet die 3er-Regel auf die gleiche Art.

Wenn wir die Teilbarkeit z.B. der Zahl 4257 durch 3 prüfen möchten, dann können wir sie folgendermaßen umformen:

4257 = 4 · 1000 + 2 · 100 + 5 · 10 + 7.

Das hilft noch nicht ganz, lässt sich aber noch weiter umformen:

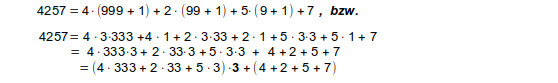
Der vordere Summand besteht aus einer Klammer (die eine natürliche Zahl ergibt) und dem Faktor 3. Damit ist dieser Summand laut Definition der Teilbarkeit durch 3 teilbar.

Die Summe aus diesem „vorderen“ Teil und der hinteren Klammer ist dann wegen Satz 1 (a und b) durch 3 teilbar, wenn die hintere Klammer durch 3 teilbar ist und sie ist nicht durch 3 teilbar, wenn die hintere Klammer nicht durch 3 teilbar ist. Die hintere Klammer ist aber genau die Quersumme der Zahl, dies liefert die Quersummenregel.
Für die Teilbarkeit durch 11 gibt es eine sogenannte „alternierende Quersummenregel“. Dazu zieht man von der Quersumme aus allen Ziffern, die an einer ungeraden Stelle stehen, die Quersumme aus allen Ziffern an geraden Stellen ab. Zum Beispiel betrachtet man für die Zahl 645 738 die Differenz von 4 + 7 + 8 und 6 + 5 + 3.

a.) Führt dies für viele Zahlen durch – sowohl durch 11 teilbare, als auch nicht durch 11 teilbare (WTR ist dabei erlaubt). Betrachtet die so gebildeten Differenzen und stellt eine Regel für die Teilbarkeit durch 11 auf.

Beispiele:

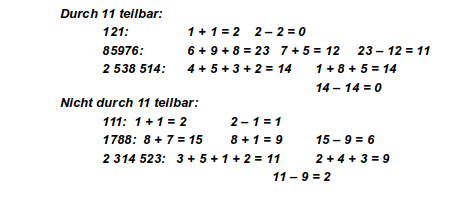
Regel:

Eine Zahl ist genau dann durch 11 teilbar, wenn die Differenz aus der Summe der Ziffern an ungeraden Stellen und der Summe der Ziffern an geraden Stellen durch 11 teilbar ist.

Übrigens: Man nennt dies die alternierende Quersumme. Denn anstatt z.B. bei der Zahl 85 976 die beiden Summen wie oben zu bilden und dann voneinander abzuziehen, kann man auch mit alternierendem Rechenzeichen so vorgehen:

8 – 5 + 9 – 7 + 6 = 11

c.)* Es gilt: 10=11−1, 100=99+1=9·11+1, 1000=1001−1=91·11−1, 10000=9999+1=909·11+1 . Begründet die Teilbarkeitsregel aus a.) mithilfe der Sätze 1 und 2 an geeigneten Aufspaltungen mit den Beispielzahlen 90981 und 53211.

Man erkennt an den Auteilungen, dass in der jeweils letzten Zeile die Summanden, die nicht fettformatiert sind, stets den Faktor 11 beinhalten und somit auch als Gesamtsumme aus selbigen) durch 11 teilbar sind. Die fett formatierten Summanden bleiben „übrig“, aus ihnen kann man wieder eine Summe bilden. Sie entspricht der alternierenden Quersumme. Wenn sie nun ebenfalls durch 11 teilbar ist, dann ist die gesamte Zahl durch 11 teilbar, ansonsten nicht.

Teilbarkeit und Teilbarkeitsregeln – Lösungen: Herunterladen [odt][394 KB]

Teilbarkeit und Teilbarkeitsregeln – Lösungen: Herunterladen [pdf][237 KB]

Weiter zu Summen und Produkte