Aussagenlogik
Die später in Klasse 9 folgende formale Behandlung aussagenlogischer Zusammenhänge wird in Klasse 8 altersangemessen mit einfachen Logikrätseln vorbereitet. Hier stehen noch exemplarische Lösestrategien und geeignete heuristische Verfahren im Vordergrund, bevor dann in Klasse 9 auch Wahrheitstafeln für zusammengesetzte logische Verknüpfungen erstellt werden und „mit der Wahrheit gerechnet“ wird. Die Aufgabe „Mördersuche“ (Nr. 4 auf dem ergänzenden Übungsblatt der 6. Stunde) wurde eingebunden, um im Rahmen der Differenzierung einen kurzen Ausblick auf die Verwendung von Wahrheitstafeln zu ermöglichen.
Auswahl der Logikrätsel
Die Auswahl der Logikrätsel für die 5. Stunde hatte wie oben beschrieben das Ziel, Graphen als heuristische Hilfsmittel einzubinden, um die Lösestrategie des Vorwärtsarbeitens übersichtlich darzustellen und den Bogen von der Graphentheorie zur Aussagenlogik zu spannen. Insbesondere Umfüllrätsel bieten dabei einige Vernetzungsmöglichkeiten, auch zur Geometrie und Physik.
Im Bildungsplan sind außerdem Sudokus, Surizas und Nonogramme als Beispiele für weitere systematische Rätsel ausgewiesen, deren Behandlung sicherlich motivierend und reizvoll ist. Da deren Lösungsstrategien aber doch eher spezifisch auf die jeweilige Rätselart ausgerichtet sind, wurde der Schwerpunkt in der 6. Stunde auf klassische Logikrätsel gelegt. Hier stehen Aussagen und Folgerungen stärker im Fokus, was für die Einführung in die Aussagenlogik günstiger erschien. Außerdem war es so auch möglich die Arbeit mit Tabellen als wichtigem heuristischen Hilfsmittel effizient zu vertiefen.
Vernetzungsbeispiel: Graphisches Lösungsverfahren für Umfüllprobleme
Am Beispiel des in Stunde 5 eingebundenen Umfüllrätsels soll hier ein interessantes graphisches Lösungsverfahren vorgestellt werden1:
Drei Krüge
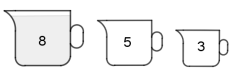
Ein Krug, der genau 8 Liter fasst, ist bis zum Rand mit Wasser gefüllt. Es stehen außerdem zwei leere Krüge mit 3 l bzw. 5 l Fassungsvermögen zur Verfügung, sonst nichts. Gelingt es euch, die 8 Liter Wasser gerecht auf zwei der Krüge zu verteilen? Wie oft müsst ihr dazu mindestens umschütten?
Das Verfahren basiert auf der Idee, in einem zugehörigen Graphen den kürzesten Kantenzug zwischen Start- und Endknoten zu finden. Dazu fasst man zunächst alle theoretisch denkbaren Füllstandskombinationen der drei Gefäße als Zustände auf. Jeder Zustand entspricht einem Tripel wie z.B. (3,4,1) und kann mithilfe von „trilinearen Koordinaten“2 als Punkt im Innern oder auf dem Rand eines gleichseitigen Dreiecks gedeutet werden. Diese Überlegung führt zu dem Dreiecksgraphen auf der folgenden Seite.
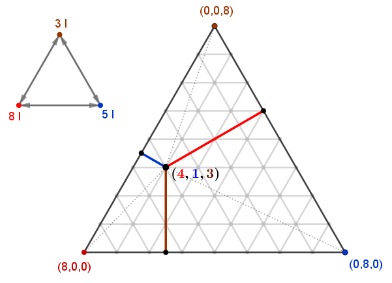
Der im Innern des Dreiecks markierte Punkt entspricht dem Zustand (4,1,3): Es befinden sich im größten Gefäß 4 Liter, im mittleren Gefäß 1 Liter und im kleinsten Gefäß 3 Liter.
Die Füllstände der Gefäße entsprechen dabei den Abständen des Punktes zu den jeweiligen Dreiecksseiten. Mithilfe der Parallelenscharen des Rasters kann man so schnell den Füllstand der einzelnen Gefäße ablesen.
Hierbei kommt die geometrische Erkenntnis zum Tragen, dass in einem gleichseitigen Dreieck die Summe der drei Abstände jedes inneren Punktes zu den drei Seiten immer gleich groß ist und der Höhe des gleichseitigen Dreiecks entspricht. Dieser Zusammenhang wird als „Satz von Viviani“ bezeichnet und kann gut mit Mitteln der 8. Klasse bewiesen werden.3 Die drei Füllstände entsprechen dabei den Maßzahlen der Höhen in den gestrichelt angedeuteten Teildreiecken. Der Beweis kann beispielsweise über die Summe der Flächeninhalte der drei Teildreiecke geführt werden und bietet eine gute Gelegenheit, geometrische Grundlagen zu wiederholen und im neuen Lichte der Aussagenlogik zu vertiefen. Es bietet sich an, diesen Beweis als Teil der Geometrieeinheit zu betrachten (vgl. BP IMP, 3.1.2.3 (4)) und von den Schülerinnen und Schülern (idealerweise nach vorheriger Erkundung mithilfe dynamischer Geometrie-Software) führen zu lassen.
Die theoretischen Füllzustände entsprechen den Knoten und die Umschüttvorgänge den (gerichteten) Kanten des abgebildeten Graphen. Dabei sind aufgrund der limitierenden Gefäßgrößen nicht alle Zustände realisierbar. Die Knoten, die mögliche Zustände (in 1-Liter-Schritten) symbolisieren, sind rechts etwas größer und grün markiert.
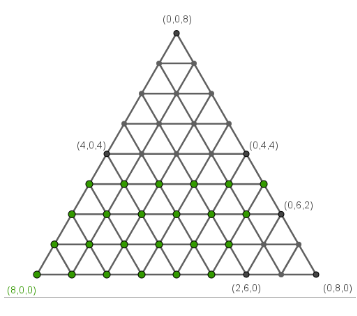
Da durch die Vorgaben des Rätsels immer so umgeschüttet wird, dass danach entweder das Ausgangsgefäß leer oder das Zielgefäß voll ist, liegen die Knoten der realisierbaren Zustände auf dem Rand des Parallelogramms.
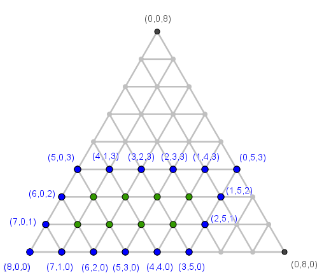
Für das eigentliche Verfahren genügt es, dieses Parallelogramm zu zeichnen (z.B. mit a = 5 LE, b = 3 LE und α = 60°):
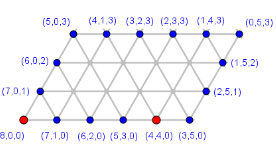
u Beginn sind im größten Gefäß 8 Liter, am Ende sollen zweimal 4 Liter vorhanden sein. Das ist nur möglich, wenn die beiden größten Gefäße jeweils 4 Liter enthalten. Die diesen Zuständen entsprechenden Start- und Zielknoten sind oben markiert. Man beginnt unten links in der Ecke, die dem Zustand (8,0,0) entspricht und visualisiert die Umschüttvorgänge durch Streckenzüge. Beim Umfüllen bleibt immer ein Gefäß unberührt, sodass man sich nur auf Parallelen zu den Dreiecksseiten bewegt. Außerdem muss beim Umfüllen immer ein Gefäß vollständig geleert oder gefüllt werden, sodass der Pfad im Parallelogramm immer bis zu dessen Rand geht. Tatsächlich ist der Kantenzug bereits durch den ersten Schritt festgelegt, alle weiteren Schritte ergeben sich automatisch4, wenn man ungünstige Umwege wie z.B. „Zurückschütten“ vermeidet.
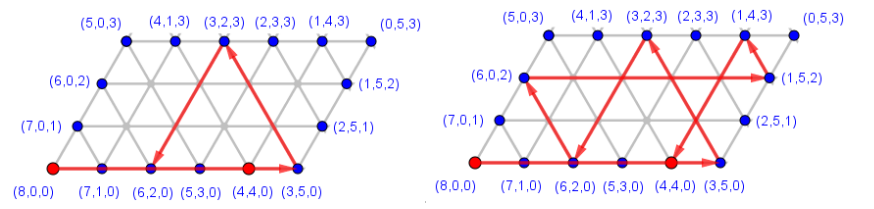
Der Pfad hat durch die Wahl des gleichseitigen Ausgangsdreiecks die Besonderheit, dass immer in einem „60°-Winkel“ abgebogen wird, der Eintritts- und Austrittswinkel in den Randpunkten also immer übereinstimmt. Man kann ihn sich dadurch auch als Weg einer fiktiven Billardkugel auf einem parallelogrammförmigen Tisch vorstellen. Der Weg dieser Kugel wird an den Kanten des Parallelogramms dann nach dem bekannten Reflexionsgesetz fortgesetzt.
Würde man den Weg über den Zielknoten (4,4,0) hinaus weiter verfolgen, so würde man die restlichen Kanten durchwandern und zum Ausgangspunkt zurückgelangen. Beginnt man dagegen den Kantenzug von Anfang an in der anderen Richtung, also durch Umschütten vom größten ins kleinste Gefäß, so gelangt man ebenfalls zum Zielknoten und erhält so die zweite mögliche Lösung. Welche der beiden die bessere ist, muss geprüft werden. Die oben abgebildete Lösung erfordert sieben Schritte.
Die zweite Lösung erfordert dagegen acht Schritte:
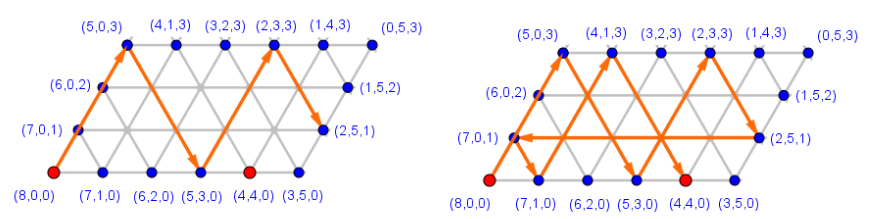
Alle anderen Vorgehensweisen enthalten unnötige Umwege. Die beiden gerichteten Kantenzüge mit sieben bzw. acht Schritten wurden in der Musterlösung des Arbeitsblattes ohne den darunterliegenden Zustandsgraphen dargestellt:

Auch wenn dieses graphische Lösungsverfahren zunächst nicht für die Behandlung im Kernunterricht vorgesehen ist, hat es Potenzial für ergänzende Phasen und differenzierende Aufträge, evtl. auch im Rahmen einer GFS. Es bietet sich die Gelegenheit, den Umgang mit Parallelogrammen zu vertiefen und ggf. Inhalte aus der Physik aufzugreifen (BP IMP, 3.1.3.1.).5 Da über den Beweis des „Satzes von Viviani“ auch die Verzahnung mit Inhalten der Geometrieeinheit möglich ist, wäre auch der direkte Bezug zum Bildungsplan gegeben.
Die Datei 05_aug_ab_umfuellgraphen_8-5-3.ggb wurde daher für eine mögliche Vorstellung im Unterricht konzipiert. Der gesamte Gedankengang kann so am Beispiel der Gefäßkombination aus Aufgabe 3 des Arbeitsblattes durch Einblenden verschiedener Knoten und Kanten schrittweise entwickelt werden. Unabhängig davon ist das Verfahren vor allem bei der Konzeption ähnlicher Umschütträtsel hilfreich.
Vertiefung der Aussagenlogik in der UE Geometrie
Die hier vorgestellten Logikrätsel und Lösestrategien sollen zur Aussagenlogik führen, die in Klasse 8 u.a. in der Geometrieeinheit im Mittelpunkt steht. Natürlich werden auch im Bereich der zahlentheoretischen Grundlagen vielfältige Aussagen betrachtet. Im Bereich der Geometrie bietet sich aber die Gelegenheit, die meisten Aussagen auch durchgängig zu visualisieren und ihren Wahrheitsgehalt unmittelbar anschaulich zu begründen. Daher spielt die Geometrie bei der Grundlegung der Aussagenlogik eine wichtige Rolle.
Im Gesamtaufbau könnte man die Geometrieeinheit daher nach der hier skizzierten Einführung direkt anschließen, um den Fokus auf die Aussagenlogik als Motivation für die erneute Behandlung scheinbar bekannter Sätze zu nutzen. Weitere Anregungen dazu finden Sie in den Materialien zur Geometrie.
1 Die Datei http://www.wiwi.uni-bielefeld.de/lehrbereiche/statoekoinf/comet/wolf/pw_files/lehrmaterialien/dist-vino.pdf (abgerufen 13.4.2018) von P. Wolf bietet Hintergrundinformationen zum skizzierten Verfahren, das von Hugo Steinhaus im „Kaleidoskop der Mathematik“ (Dt. Verl. d. Wiss.,1959) publiziert wurde.
2 Wikipedia: siehe Seite „Trilineare Koordinaten“,URL: https://de.wikipedia.org/wiki/Trilineare_Koordinaten" (abgerufen: 7.05.2018)
3 Wikipedia, Seite „Satz von Viviani", URL: https://de.wikipedia.org/wiki/Satz_von_Viviani (abgerufen:7.5.2018)
4 Vgl. Fußnote 1, in der dort angegebenen Datei wird der Hintergrund ausführlich dargestellt.
5 Einfalls- bzw. Ausfallswinkel sind Winkel zwischen Strahl und „Lot“ (Orthogonale zur Kante im Auftreffpunkt), beim Billiard steht dagegen der Winkel von Strahl und Kante im Fokus, dieser Aspekt sollte geklärt werden.
Hintergrundinformationen: Herunterladen [odt][526 KB]
Hintergrundinformationen: Herunterladen [pdf][451 KB]
Weiter zu Anhang
