Beispiel
Infobox
Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Bitte beachten Sie, dass der Bildungsplan fortgeschrieben wurde.
Ein Beispiel aus dem Themenkreis Parallelogramm soll die Abstufungen der „Begründungskompetenz“ illustrieren.
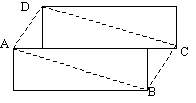Problemstellung:
Aus zwei übereinander gelegten Blättern Papier werden zusammen zwei Rechtecke ausgeschnitten. Die Rechtecke werden an jeweils längeren Seiten aneinandergelegt und ein Stück verschoben.
Handelt es sich bei dem Viereck ABCD um ein besonderes Viereck? Begründe!
In jeder Stufe der Entwicklung sollten Beispiele gezeichnet und daraus die Vermutung gewonnen werden: Beim Viereck ABCD muss es sich um ein Parallelogramm handeln.
Diese Vermutung kann nun auf ganz verschiedenen kognitiven Stufen begründet werden.
Stufe 1:
Die Schüler verbinden mit dem Begriff „Parallelogramm“ das Phänomen
der Gesamtfigur, des gezeichneten Objekts. Dieser Erkenntnisstand ist propädeutisch,
eine logische Strukturierung fehlt völlig. Man „sieht“ es einfach.
Stufe 2:
Die Schüler beziehen sich bei der Beurteilung, ob
ein Parallelogramm vorliegt, nicht mehr nur auf die Figur. Sie wissen, dass
das ein Parallelogramm bestimmte Eigenschaften haben muss, die sie aber zunächst
als Auflistung formulieren:
„Bei einem Parallelogramm sind gegenüberliegende Seiten gleich lang und parallel
und gegenüberliegende Winkel sind gleich weit und die Diagonalen halbieren
sich und ...“. Diese Eigenschaften werden durch Nachmessen oder anschauliche
Begründungen
„nachgewiesen“. Eine Trennung in eine definierende Eigenschaft und sich daraus
ergebende Eigenschaften hat noch nicht stattgefunden. Das ist etwa der Stand
in Klasse 5.
Stufe 3:
Die Schüler wissen (ohne formale Begründung), dass
man von einem Viereck nicht alle der oben angeführten Eigenschaften
wissen muss, um auf ein Parallelogramm zu schließen.
Es genügt z.B.
(i) Das Viereck hat zwei Paare paralleler Gegenseiten oder
(ii) Das Viereck hat ein Paar paralleler und gleich langer Gegenseiten oder
(iii) Das Viereck hat zwei Paare gleich langer Gegenseiten oder ...
Die anderen Eigenschaften folgen dann „automatisch“.
Vielleicht kann man auch schon Sachverhalte in der „Wenn. ..., dann ...„ -Form formulieren: „Wenn in einem Viereck gegenüberliegende Seiten gleich lang sind, dann sind gegenüberliegende Seiten parallel“ usw..
Jetzt sind erste Beweise auf der Basis von Abbildungen bzw. Symmetrie möglich (etwa gegen Ende der Klasse 6):
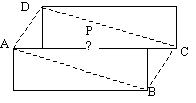3a) Ein Sch. könnte sagen: Das obere Rechteck
geht aus dem unteren Rechteck mittels einer Punktspiegelung an P (Mitte von
AC) hervor. (Diese Aussage spielt jetzt die Rolle eines Axioms.) B wird auf
D gespiegelt, A auf C. Die Strecken AB und DC sind deshalb gleich lang und
parallel, das ergibt sich aus den Eigenschaften der Punktspiegelung.
3b) Ein Sch. könnte auch anschaulich mit einer Verschiebung argumentieren (nicht
im Kerncurriculum).
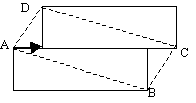Das obere Rechteck ist aus dem unteren Rechteck
durch Verschiebung mit dem eingezeichneten Pfeil entstanden. (Diese Aussage
spielt jetzt die Rolle eines Axioms.)
Beim Verschieben bleiben Streckenlängen und Winkelweiten gleich, also sind AB und DC parallel und gleich lang.
Man sieht in beiden Fällen: Hier gibt es zum ersten Mal ein „Weil ..., also ...“, ein erster Schritt zum deduktiven Denken.
Stufe 4:
In Stufe 3 wurden die Abbildungen als Beweismittel eingesetzt.
Dabei können die Begründungsketten nicht immer zufriedenstellend aufgebaut werden.
Dies wird in Klasse 7 besser, wenn die ersten Beweismittel in Satzform zur Verfügung
stehen.
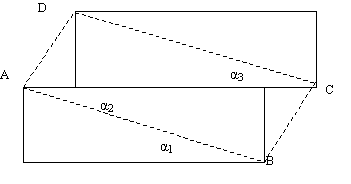Zeige mit Hilfe der Sätze vom Stufen- und
Wechselwinkel, dass das Viereck ABCD ein Parallelogramnm ist.
Wir zeigen:
AB parallel zu DC und AB = DC.
(i) AB = DC, da es sich um deckungsgleiche Rechtecke handelt.
(ii) α
2
= α
1
(WW an parallelen Rechtecksseiten)
α
3
= α
1
(Entsprechender Winkel in
deckungsgleichen Rechtecken)
Also α
2
= α
3
.
Also AB parallel DC (WW an AC).
(Hier liegt der Schülerfehler nahe, Voraussetzung und Behauptung zu vertauschen:
α
2
= α
3
(WW), also AB parallel DC )
Stufe 5:
Der Gipfel des Anspruchs wäre erreicht, wenn Schüler stellenweise
in der Lage sind, eine solche Vermutung zielgerichtet deduktiv zu begründen
bzw. ein Problem zielgerichtet zu lösen. Zielgerichtet bedeutet: Die Beweismittel
„fallen nicht vom Himmel“, sondern sind Ergebnis strukturierten Nachdenkens.
Der Schüler würde dann etwa sagen (Ende Klasse 8): „Ich will Parallelität nachweisen. Dazu habe ich folgende Sätze zur Verfügung: Satz vom Stufenwinkel; Satz vom Wechselwinkel, Satz vom Parallelogramm, die Kongruenzsätze (später auch Strahlensätze). Mit diesen Sätzen muss ich jetzt argumentieren. Ich warte nicht darauf, dass eine Beweisidee vom Himmelfällt, sondern ich versuche, gezielt diese Sätze anzuwenden.“ Z.B.
a) “Ich suche nach kongruenten Dreiecken.“
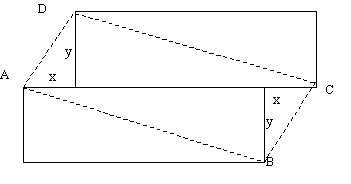Die beiden kleinen Dreiecke sind nach dem Kongruenzsatz sws kongruent.
Also stimmen sie in allen entsprechenden Teilen überein.
Es ist AD = BC. Auch entsprechende Winkel sind gleich usw.
Das wäre jetzt „Vorwärtsarbeiten“. Beim „Rückwärts arbeiten“ ginge das so:
Ich will AD parallel BC nachweisen. Dazu benötige ich zwei gleiche Winkel an der Gerade AC (Wechselwinkelsatz). Diesen Nachweis kann ich mit Hilfe kongruenter Dreiecke führen usw.
b) „Ich verwende den Pythagoras, weil es viele rechtwinklige Dreiecke hat.“
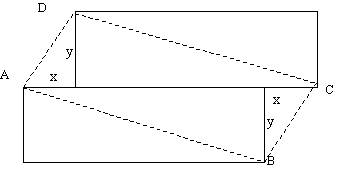Mit dem Satz des Pythagoras erhält man leicht
AB = DC und AD = BC.
Wie komme ich jetzt von gleichlangen Gegenseiten auf parallele Gegenseiten? Gibt es dafür Sätze?
Man sieht, dass auf dieser Stufe das Beweisen offen unterrichtet werden kann im Sinne von „es gibt verschiedenen fachliche Zugänge zum Beweis“. Das gilt für die überwiegenden Anzahl geometrischer Problemstellungen. Voraussetzung für einen solchen Unterricht ist natürlich die Kenntnis des Lehrers im Hinblick auf diese Fachmethoden (Beweismittel) und der Wille, die Wege zu einem Satz (einer Problemlösung) zu thematisieren, zu vergleichen und zu bewerten.
Dabei soll klar gesagt werden: Diese Strukturierungsvorschläge wollen eine Diskussionsgrundlage bieten. Sie müssen, wie alle didaktischen Überlegungen, an der schulischen Wirklichkeit gemessen werden. Aber gültig bleibt: Wir Lehrer müssen eine Strukturierung bewusst auswählen, sie den Schülern sichtbar machen und den Inhalten damit in einem Gesamtgefüge einen Sinn und Bedeutung zumessen. Sonst können wir unseren Schülern nicht vermitteln, was uns an dieser Wissenschaft begeistert.
Logisch-deduktiv strukturieren – Eine kognitive Herausforderung:
Herunterladen
[pdf]
[358 KB]