Mittelsenkrechte
Infobox
Diese Seite ist Teil einer Materialiensammlung zum Bildungsplan 2004: Grundlagen der Kompetenzorientierung. Bitte beachten Sie, dass der Bildungsplan fortgeschrieben wurde.
1. Ein Beispiel zum „Lokalen Ordnen“: Mittelsenkrechte .
In Schulbüchern findet man zur Mittelsenkrechten Formulierungen wie:
Die Mittelsenkrechte einer Strecke AB ist die Menge aller Punkte,
die von A und B den gleichen Abstand haben.
oder
Die Mittelsenkrechte einer Strecke ist die Ortslinie aller Punkte,
die von den Endpunkten der Strecke den gleichen Abstand haben.
Solche Formulierungen sind logisch nicht klar strukturiert. Sie sind mehr oder
weniger eine Situationsbeschreibung, die dem Entwicklungsstand der Schüler gerecht
zu werden versucht. Die Schüler sehen zunächst noch die gesamte Figur als Einheit
an, d.h. der gleiche Abstand von A und B zu P ist untrennbar mit der Lage von
P auf der Mittelsenkrechten verbunden. Beide Situationen („
“
und „P liegt auf der Mittelsenkrechten“) treten für den Schüler sozusagen gleichzeitig
auf, ein kausaler Zusammenhang ist seinem Denken zunächst noch fremd.
Könnte man an dieser Stelle auch beginnen, den Sachverhalt deduktiv zu ordnen und das übergeordnete Lernziel „mathematisch begründen und argumentieren“ verfolgen?
Dazu muss zunächst geklärt werden, wie ein deduktiv korrekter Aufbau ohne Rücksicht auf die Schule aussehen würde. Danach kann diskutiert werden, ob und wie dies in der Schule machbar ist.
Eine deduktiv korrekte Einführung des Begriffs „Mittelsenkrechte“, die nur Kenntnisse aus Klasse 5/6 (Symmetrie und Abbildungen) verwendet, könnte so aussehen:
Definition:
Zu einer Strecke AB heißt eine Gerade m
Mittelsenkrechte
, wenn sie durch
die Mitte von AB verläuft und zu AB orthogonal ist.
Satz 1:
Wenn ein Punkt P auf der Mittelsenkrechten m von A und B liegt, dann
hat P von A und von B den gleichen Abstand.
Beweis:
m ist die Symmetrieachse von AB. P liegt nach Voraussetzung auf m. Deshalb
wird die Strecke AP auf die Strecke BP gespiegelt. Also sind diese Strecken
gleich lang.
Hier wird als Vorwissen bzw. Beweismittel benutzt:
a) Die Mittelsenkrechte einer Strecke AB ist Symmetrieachse von AB.
b) Symmetrisch liegende Punkte (hier A und B) werden aufeinander gespiegelt;
ein
Punkt auf der Symmetrieachse (hier P) wird auf sich gespiegelt.
c) Liegen zwei Strecken (hier AP und BP) achsensymmetrisch zueinander,
dann
sind sie gleich lang.
Satz 2:
Wenn ein Punkt P von zwei Punkten A und B den gleichen Abstand hat, dann liegt
P auf der Mittelsenkrechten m von AB.
Beweis:
Mit Kontradiktion. Man zeigt:
Liegt ein Punkt Q nicht auf m, dann ist
.
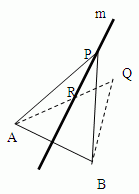Nachweis: O.B.d.A. liege B wie in der Figur
Rechts von m. R sei der Schnittpunkt von
AQ mit m.
Es ist
(Dreiecksungleichung)
und
.
Also
;
.
Didaktische Bewertung:
Satz 1 und Satz 2 sind Satz und Kehrsätze. Beide Richtungen werden in der Schulgeometrie gebraucht.
Was kann in der Schule geleistet werden ?
a) Die Formulierung der Aussagen in „Wenn . . . , dann . . . „ - Form.
b) Die Formulierung beider Richtungen und eine Begründung von Satz 1 mittels Eigenschaften der Geradenspiegelung bzw. der Achsensymmetrie.
Die getrennte Formulierung von Satz und Kehrsatz ist m.E. ein bedeutender kognitiver Anspruch und sollte in geeigneter Weise eingeübt werden. (Siehe der folgende Satz 2)
Nicht (oder kaum) leisten kann man in der Schule in Klasse 7 einen formal auf die Kontradiktion abhebende Begründung von Satz 2, dazu hin noch mit dem subtilen Argument der Dreiecksungleichung.
Die Verwendung der Mittelsenkrechten beim Thema Umkreis zeigt, wie man dieses logische Vorwissen verwenden und vertiefen kann.
Logisch-deduktiv strukturieren – Eine kognitive Herausforderung:
Herunterladen
[pdf]
[358 KB]